根根据光纤横截面上折射率的径向分布情况，可以将光纤粗略地分为阶跃（SI）光纤和渐变（GI）光纤。阶跃光纤折射率在纤芯为n1保持不变，到包层突然变为n2，如图3.1.4a所示。渐变光纤折射率n1不像阶跃光纤是个常数，而是在纤芯中心最大，沿径向往外按抛物线形状逐渐变小，直到包层变为n2，如图3.1.4b所示。
渐变多模光纤的折射率分布可使光纤内的光线同时到达终点，其理由是，虽然各模光线以不同的路径在纤芯内传输，但是因为这种光纤的纤芯折射率不再是一个常数，所以各模的传输速度也互不相同。如图3.1.5所示，沿光纤轴线传输的光线速度最慢（因n1,r→0最大，所以速度c/n1,r→0最小）；光线3到达末端传输的距离最长，但是它的传输速度最快（因n1,r→a最小，所以速度c/n1,r→a最大），这样一来到达终点所需的时间几乎相同。n1,r→0表示纤芯折射率从包层变化到纤芯，n1,r→a表示纤芯折射率从纤芯变化到与包层交界处。
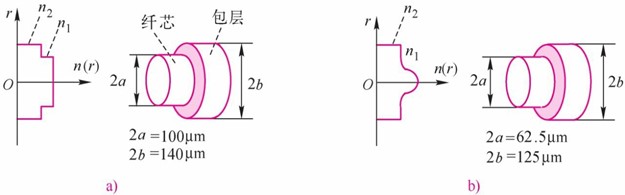
图3.1.4 阶跃光纤和渐变光纤
a）阶跃光纤b）渐变光纤
为了进一步理解渐变多模光纤的传光原理，我们可把这种光纤看作由折射率恒定不变的许多同轴圆柱薄层a、b和c等组成，如图3.1.6a所示，而且na>nb>nc>…。使光线1的入射角θA正好等于折射率为na的a层和折射率为nb的b层的交界面A点发生全反射时的临界角θc（ab）=arcsin（nb/na），然后到达光纤轴线上的O′点。而光线2的入射角θB却小于在a层和b层交界面B点处的临界角θc（ab），因此不能发生全反射，而光线2以折射角θB′折射进入b层。如果nb适当且小于na，光线2就可以到达b和c界面的B′点，它正好在A点的上方（OO′线的中点）。假如选择nc适当且比nb小，使光线2在B′发生全反射，即θB′>θC（bc）=arcsin（nc/nb）。于是通过适当地选择na、nb和nc，就可以确保光线1和光线2通过O′。那么，它们是否同时到达O′呢？由于na>nb，所以光线2在b层要比光线1在a层传输得快，尽管它传输得路径比较长，也能够赶上光线1，所以几乎同时到达O′点。这种渐变多模光纤的传光原理，相当于在这种波导中有许多按一定规律排列的自聚焦透镜，把光线局限在波导中传输，如图3.1.5所示。
实际上，渐变光纤的折射率是连续变化的，所以光线从一层传输到另一层也是连续的，如图3.1.6b和图3.1.6c所示。当光线经多次折射后，总会找到一点，其折射率满足全反射。
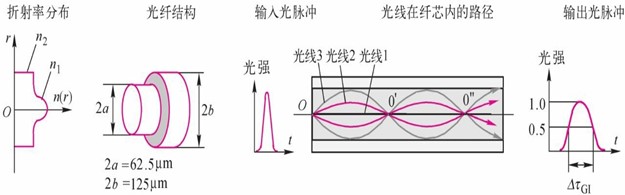
图3.1.5渐变折射率多模光纤的结构、折射率分布和在纤芯内的传输路径
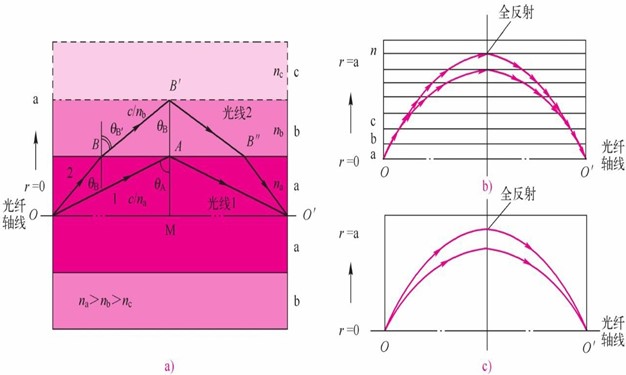
图3.1.6 渐变多模光纤内光线传输路径不同但同时到达终点
