学习知识要善于思考,思考,再思考。我就是靠这个方法成为科学家的。 —爱因斯坦(A.Einstein)
一、接收机比特误码率(BER)
数字接收机的性能指标由比特误码率(BER)决定,定义BER为码元在传输过程中出现差错的概率,工程中常用一段时间内出现误码的码元数与传输的总码元数之比来表示。例如,BER=10-6,表示每传输百万比特只允许错1比特;如BER=10-9,则表示每传输10亿比特只允许错1比特。通常,数字光接收机要求BER≤10-9。此时,定义接收机灵敏度为保证比特误码率为10-9时,要求的最小平均接收光功率(Prec)。假如一个接收机用较少的入射光功率就可以达到相同的性能指标,那么可以说该接收机更灵敏些。影响接收机灵敏度的主要因素是各种噪声。
由于超强前向纠错(SFEC)和电子色散补偿的应用,使纠错能力大为提高,当Q=6.3dB时,容许系统送入纠错模块前的BER甚至可以达到2×10-2。
二、比特误码率用Q参数表示
二、比特误码率用Q参数表示
图7.3.1为噪声引起信号误码的图解说明。由图可见,由于叠加了噪声,使“1”码在判决时刻变成“0”码,经判决电路后产生了一个误码。
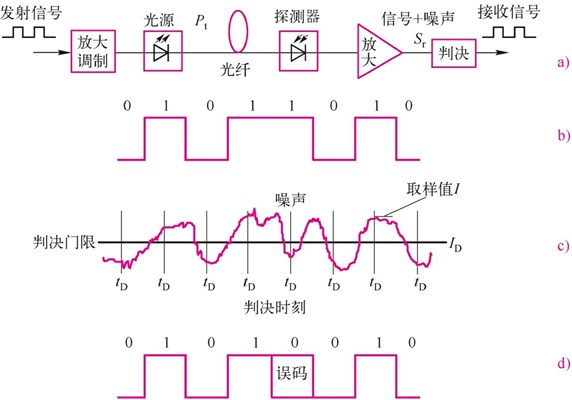
图7.3.1噪声引起误码的图解说明
a)系统构成b)发射信号Pt(t)c)在接收端探测到的带有噪声的接近升余弦波形的信号Sr(t)
d)由于噪声叠加,使“1”码在判决时刻变成“0”码,经判决电路后产生了一个误码
图7.3.1c表示判决电路接收到的信号,由于噪声的干扰,在信号波形上已叠加了随机起伏的噪声。判决电路用恢复的时钟在判决时刻tD对叠加了噪声的信号取样。等待取样的“1”码信号和“0”码信号分别围绕着平均值I1和I0摆动,如图7.3.2所示。判决电路把取样值与判决门限ID比较,如果I>ID,认为是“1”码;如果I<ID,则认为是“0”码。由于接收机噪声的影响,可能把比特“1”判决为I<ID,误认为是“0”码;同样也可能把“0”码错判为“1”码。误码率包括这两种可能引起的误码,因此误码率为
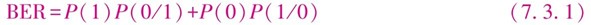
式中,P(1)和P(0)分别是接收“1”和“0”码的概率,P(0/1)是
把“1”判为“0”的概率,P(1/0)是把“0”判为“1”的概率。对脉冲编码调制(PCM)比特流,“1”和“0”发生的概率相等,P(1)=P(0)=1/2。因此比特误码率为

图7.3.2a表示判决电路接收到的叠加了噪声的PCM比特流,图7.3.2b表示“1”码信号和“0”码信号在平均信号电平I1和I0附近的高斯概率分布,阴影区表示当I1<ID或I0>ID时的错误识别概率。
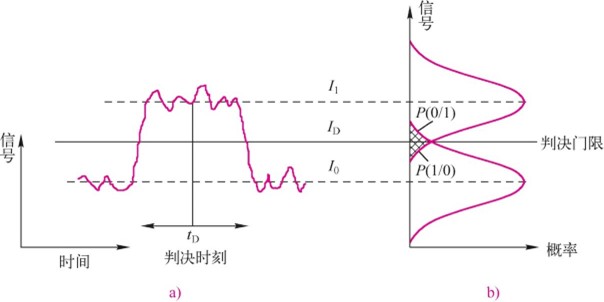
图7.3.2二进制信号的误码概率计算
a)判决电路接收到的叠加了噪声的PCM比特流,判决电路在判决时刻tD对信号取样
b)“1”码信号和“0”码信号在平均信号电平I1和I0附近的高斯概率分布,阴影区表示当I1<ID或I0>ID时的错误识别概率
可以证明,最佳判决值的比特误码率为
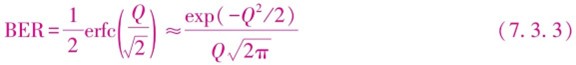
式中

σ1表示接收“1”码的噪声电流,σ0表示接收“0”码时的噪声电流,erfc代表误差函数erf(x)的互补函数。
图7.3.3表示Q参数和比特误码率(BER)及接收到的信噪比(SNR)的关系,信号用峰值(pk)功率表示,噪声用均方根噪声(rms)功率表示。由图可见,随Q值的增加,BER下降,当Q>7时,BER<10-12。因为Q=6时,BER=10-9,所以Q=6时的平均接收光功率就是接收机灵敏度。近来超强前向纠错(SFEC)和电子色散补偿的应用,使纠错能力大为提高。
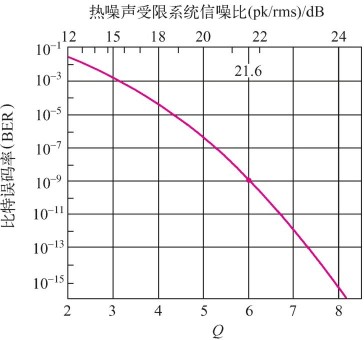
图7.3.3Q参数和比特误码率及接收到的信噪比的关系
三、Q参数和信噪比(SNR)的关系——Q的平方等于SNR
把简单的事情考虑得很复杂,可以发现新领域;把复杂的现象看得很简单,可以发现新定律。
——牛顿(I.Newton)
比特误码率(BER)表达式(7.3.3)可被用来计算最小接收光功率,所谓最小接收光功率是指BER低于指定值使接收机可靠工作所需要的功率,为此,应建立Q与入射光功率的关系。为了简化起见,考虑“0”码时不发射光功率,即P0=0,I0=0。“1”码功率P1与电流I1的关系为
比特误码率(BER)表达式(7.3.3)可被用来计算最小接收光功率,所谓最小接收光功率是指BER低于指定值使接收机可靠工作所需要的功率,为此,应建立Q与入射光功率的关系。为了简化起见,考虑“0”码时不发射光功率,即P0=0,I0=0。“1”码功率P1与电流I1的关系为

式中,R是光探测器响应度,是平均接收光功率,定义为P=(P1+P0)/2,M为APD雪崩增益倍数。M=1为PIN接收机。
噪声电流σ1和σ0包括由式(7.2.2)和式(7.2.3)给出的散粒噪声σs和热噪声σT项。σ1和σ0的表达式分别是

将式(7.3.5)和式(7.3.6)代入式(7.3.4),可得到
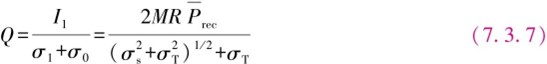
对于指定的BER,由式(7.3.3)求得Q值。对于给定的Q值,解式(7.3.7),可得到平均接收光功率

在受热噪声限制的接收机中,σ1 ≈σ0,使用I0=0,式(7.3.4)变为Q=I1/2σ1,式(7.2.1)变为

因为BER=10-9时,Q=6,所以SNR必须至少为144或21.6dB。
在散粒噪声受限的系统中,σ0 ≈0,假如暗电流的影响可以忽略,“0”码的散粒噪声也可以忽略,此时Q=I1/σ1=(SNR)1/2,或

于是,可得到信噪比与Q的简单表达式。
为了使BER=10-9,SNR=36或15.6dB就足够了。由式(7.2.4)可知,SNR=ηNP,所以Q=(ηNP)1/2,把此式代入式(7.3.3)中,得到受散粒噪声限制的系统比特误码率为
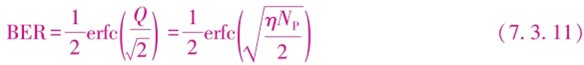
对于100%量子效率的接收机(η=1),当NP=36时,BER=10-9。实际上,大多数受热噪声限制的系统,要想达到BER=10-9,NP必须接近1000。
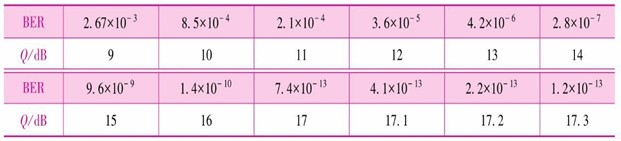
由式(7.3.3)、式(7.3.11)和图7.3.3可知,BER与Q值有关。由式(7.3.10)可知,Q2正好等于SNR。所以,通常使用Q值的大小来衡量系统性能的好坏。在工程应用中,通过测量BER,计算Q值,Q值与BER换算如表7.3.1所示。
表7.3.1Q值与BER对照表
四、 Q参数和光信噪比(OSNR)的关系——Q的平方等于OSNR
在7.3.2节和7.3.3节,已经推导出BER与Q参数、Q参数与SNR的关系(分别见式(7.3.3)和式(7.3.10)),本节把影响Q参数的更多因素考虑进去,来推导Q参数与光信噪比(OSNR)的关系式。
在偏振复用系统中,传输性能被信号与ASE拍频噪声所限制,此时可忽略接收机热噪声和散粒噪声的影响,并把消光比rEXR=P0/P1的影响考虑进去,此时式(7.3.4)Q参数表达式变为

假如发送机的I0=0,消光比rEXR=P0/P1=0,在信号与ASE拍频噪声限制系统中,可认为σ0≈0,此时式(7.3.12)变为Q=I1/σ1=(OSNR)1/2,即

由此可见,Q2正好等于光信噪比(OSNR),这和7.3.3节得出的Q2等于信噪比(SNR)一样。因此通常使用Q参数来衡量系统性能的好坏,Q值越大,OSNR越大,BER越小(见图7.3.3)。如用dB表示Q,则=10lgQ2=10lg(OSNR)。
当考虑调制方式的影响时

式中,m是调制深度,与发送机消光比rEXR有关,定义
。同时m也与调制方式有关,NRZ码,m=1;RZ码,m=1.4。该系数也与光、电滤波器传输函数有关。
在工程应用中,通过对Q值测试,利用式(7.3.13)计算OSNR。Q值与BER的关系如图7.3.3所示,其换算如表7.3.1所示。
对于偏振复用QPSK调制系统,BER和OSNR的关系是

此时,把非线性影响作为增加的白高斯噪声。将式(7.3.15)代入式(7.3.13),可以得到Q与BER的关系