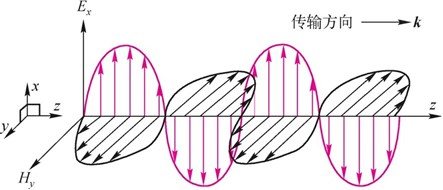
图中,行波沿矢量k传播,k称为波矢量,它的幅度是传播常数k=2π/λ,显然,它与恒定的相平面(波前)垂直。波矢量k的传播方向可以是任意方向,也可以与z不一致。
根据式(2.2.1),在给定的时间(t)和空间(z),对应最大场的相位φ可用下式描述:
φ=(ωt-kz+φo)
在时间间隔δt,波前移动了δz,因此该波的相速度是δz/δt。于是相速度为

式中,ν是频率(ω=2πν),单位是赫兹(Hz),1Hz等于每秒振荡1周,两个相邻振荡波峰之间的时间间隔称为周期T,等于光波频率的倒数,即ν=1/T。
假如波沿着z方向依波矢量k传播,如式(2.2.1)所示,被Δz分开的两点间的相位差Δφ可用kΔz简单表示,因为对于每一点ωt是相同的。假如相位差是0或2π的整数倍,则两个点是同相位,于是相位差Δφ可表示为

我们经常对光波上给定时间被一定的距离分开的两点间的相位差感兴趣,比如由马赫-曾德尔(MZ)干涉仪构成的滤波器、复用/解复用器和调制器,由阵列波导光栅(AWG)构成的诸多器件(滤波器、波分复用/解复用器、光分插复用器和波长可调/多频激光器等),以及由电光效应制成的外调制器和由热光效应制成的热光开关等,它们的工作原理均用到相位差的概念,所以大家要特别予以关注,之后有关章节也会经常用到这一概念,并使用式(2.2.3)。