1. 一、二进制数字调制抗噪分析
通信系统的抗噪声性能是指系统克服加性噪声的能力。在数字通信中,信道加性噪声有可能使传输码元产生错误。这种传输错误通常用误码率来衡量。所以,在分析数字调制系统的抗噪声性能时,就是求出系统在加性噪声作用下的总误码率。
1.二进制振幅键控系统的抗噪声性能
设2ASK系统中发送一个码元时间Ts内波形为
而接收波形为
2ASK信号可以采用包络检波和相干解调法进行解调,在解调器前端都需经过一个带通滤波器,其输出波形为
ni(t)为经过带通滤波器后的噪声,为一个窄带高斯白噪声,可知
ni(t)=nc(t)cosωct-ns(t)sinωct
则有
1)包络检波法的系统性能
由yi(t)表达式可知,经包络检波和低通滤器后输出包络为
由随机信号分析可知,发送1码的包络函数其一维概率密度函数服从广义瑞利分布;发送0码的包络函数其一维概率密度函数服从瑞利分布。
式中,  为n(t)的方差。
为n(t)的方差。
如图2-16所示,当发送为“1”码时,判决为“0”码的差错概率为
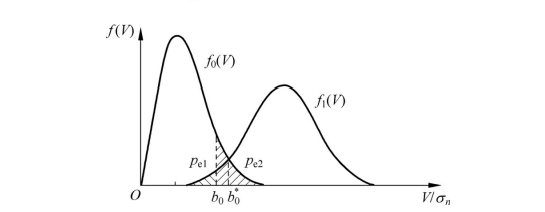
图2-16 2ASK“0”误判率概率示意图
为计算上式积分值,引入特殊函数——Q函数(Marcum函数),该函数定义为
则有
式中, 为信号与噪声的平均功率比,称为信噪比;
为信号与噪声的平均功率比,称为信噪比; 为归一化门限值。
为归一化门限值。
同理,当发送“0”码时,判决为“1”码的差错概率为
设发送“1”码的概率为p(1),发送“0”码的概率为p(0),则系统总误码率为
设发送“1”码的概率为p(1),发送“0”码的概率为p(0), 则系统总误码率为
当 时,
时,
在大信噪比情况下,即 ,表达式可简化为
,表达式可简化为
对于大信噪比时, ,再利用Q函数的特殊值,化简得到
,再利用Q函数的特殊值,化简得到
当x→∞时erfc(x)→0;故式(2-4)中r→∞时,变为
式(2-4)是在大信噪比条件下、最佳门限电平判决以及p(1)=p(0)条件下得到的,它表明ASK系统总误码率pe随着信噪比r的增加而近似地按指数规律下降。
2)相干解调法的系统性能
接收波形与相干载波相乘,然后由低通滤波器滤除载频的二次谐波,抽样判决输入波形为
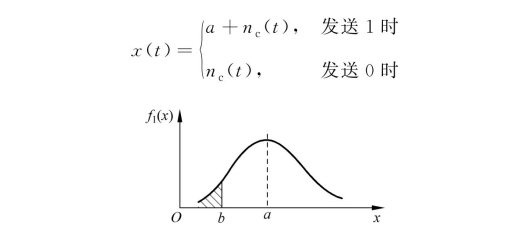
图2-17 发送“1”高斯概率分布图
如图2-17所示,由于nc(t)是高斯过程,因此当发送“1”时,过程a+nc(t)的一维概率密度为
如图2-18所示,而当发送“0”时,nc(t)的一维概率密度为
如图2-19所示,若令判决门限电平值为b,则发送码元1错判为0(如图2-19中b'所示)的概率为
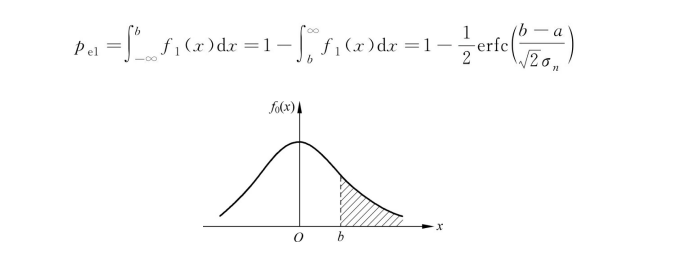
图2-18发送“0”高斯概率分布图
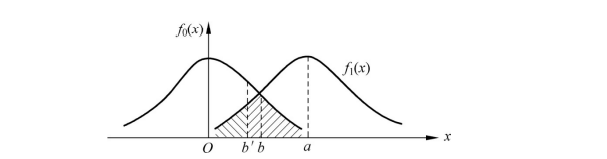
图2-19 高斯概率分布误判示意图
同理,可求得发送0码错判为1码的概率为
可确定最佳门限电平x*=a/2,或最佳归一化门限电平 。
。
在发送码元1和0概率相等的情况下,则可得系统总误码率为
2ASK系统总误码率为
当r≫1时,式(2-6)变为
2.二进制移频键控系统的抗噪声性能
设2FSK系统的发送信号在一个码元时间Ts内的波形为
2FSK信号解调采用包络检波法和相干解调法,在解调过程中,每一系统用两个带通滤波器来区分中心频率为ω1和ω2的信号码元。假设带通滤波器无失真地使信号通过,则输出端波形为
式中,;
 为窄带高斯过程。
为窄带高斯过程。
1)包络检波系统性能
假设(0,Ts)时间内所发送的码元为“1”(对应ω1),则这时送入抽样判决器的两路输入包络信号分别为
发送0码元时两包络信号分别为
由v1(t)和v2(t)的4个式子相比较可以看出,所得误码率具有完全相同的结果pe1=pe2,因此只需要计算发送码元1时的误码率即可。
根据上面的讨论可知,v1(t)的一维概率分布为广义瑞利分布,而v2(t)的一维概率分布为瑞利分布。在判决时,当v1(t)的取样值V1小于v2(t)的取样值V2时,则发生错误判决,其错误概率为
根据Q函数性质有 于是上式pe1为
于是上式pe1为
式中, 。
。
同理,可求得发送0码错判为1码的概率为
于是2FSK信号传输非相干接收系统总误码率为
2)相干解调系统性能
接收的2FSK信号经与相干载波相乘,并经低通滤波器,输入到判决器的两路信号在码元1时为
在码元为0时为
因为n1c(t)和n2c(t)分别是窄带高斯过程的同相分量,所以它们也是高斯过程。
信号为1码时,抽样值x1=a+n1c(t)是均值为a、方差为  的高斯变量;抽样值x2=n2c,也是均值为0、方差为 的高斯变量;若抽样值x1>x2,则判为1码;反之,则判为0码。发送1码时,若x1<x2,则误判为0码,故误码率为
的高斯变量;抽样值x2=n2c,也是均值为0、方差为 的高斯变量;若抽样值x1>x2,则判为1码;反之,则判为0码。发送1码时,若x1<x2,则误判为0码,故误码率为
pe1=p(x1<x2)=p[(a+n1c)<n2c]=p(a+n1c-n2c<0)
令z=a+n1c-n2c,则z也是高斯变量,且均值为a,方差为 ,则
,则
于是z的一维概率度为
总误码率为
由于pe2=pe1,在发送码元1和0等概率条件下,即
于是2FSK系统总误码率为
在大信噪比条件下,式(2-9)简化为
3.二进制相移键控及差分相移键控系统的抗噪声性能
1)2PSK系统极性比较法性能
参照2ASK系统相干解调并假设判决门限为0电平,则在一个码元持续时间内,可直接写出低通滤波器输出波形
它们的一维概率密度是分布在x=0两边的完全对称的高斯分布,均值分别为a和-a,方差均为 。当发送1码时,若判决值x<0,将发生“1”判为“0”的错误,其错误概率pe1为pe1=p(x<0)。同理,将“0”判为“1”的错误概率为pe2=p(x>0)。因为pe1=pe2,只求pe1即可。
式中, 。
。
因为pe1=pe2,故2PSK信号极性比较法解调时系统总误码率为
在大信噪比情况下:
2)2DPSK系统相位比较法性能
相位比较法与极性比较法的重要区别在于前者的参考信号不再像后者那样具有固定的载频和相位,此时它是受到加性噪声干扰的。因此,设在一个码元时间内发送的是1码,且令前一个码元也为1码(也可为0码),则在鉴相器的两路波形为
y1(t)=[a+n1c(t)]cosωct-n1s(t)sinωct
y2(t)=[a+n2c(t)]cosωct-n2s(t)sinωct
式中,y1(t)为无迟延支路波形;y2(t)为迟延支路波形。理想鉴相器为相乘-低通滤波器,则输出为
对x(t)进行抽样判决,x>0判为1码,x<0判为0码。
利用恒等式
利用恒等式
则发送1码时,将1码错判为0码的概率为
设:
则有pe1=p(R1<R2)。
因为n1c、n2c、n1s、n2s均为高斯变量,由以前讨论可知R1服从广
义瑞利分布,R2服从瑞利分布,其概率密度分别为
可得
同理,“0”错判为“1”的概率pe2=pe1。
因此,2DPSK系统相位比较法总误码率为
因此,2DPSK系统相位比较法总误码率为
2DPSK信号的解调还可以采用极性比较法,与2PSK信号极性比较法不同的就是在2PSK解调后再加一个码反变换器。因此,2DPSK极性比较法的误码率应在2PSK信号极性比较法的基础上再考虑码反变换器所造成的误码率。
由码反变换器的相关知识可以得出,若相干解调输出一个或多个连续错码,在码反变换器输出都会引起两个错码,经计算可以推出结论:在2PSK系统中加上码反变换器后将会使其总误码率增加,因此2DPSK信号极性比较法总误码率为
2. 2.1.4二进制数字调制系统的性能比较
综合前面的讨论,对二进制数字信号频带传输系统的抗噪声性能已经有所了解。下面针对系统的频带宽度、误码率及对信道特性变化敏感性等几方面加以简单比较。
1.误码率分析
误码率(SymbolErrorRate,SER)是衡量数据在规定时间内数据传输精确性的指标,误码率=(传输中的误码/所传输的总码数)×100%。在使用二进制编码时误码率等于比特差错概率(BitErrorProbability)。在通信系统中,误码率是非常关键的参数,有时也用误包率(PacketError Rate,PER)表示。在表达一片芯片的灵敏度时,都会标注其测试环境的误码率或误包率。
例如,一个数据包采用二进制编码,长度为10b,其误码率为0.1%,则其误包率约为1%,计算公式为
式中,pb为误包率;pe为误码率;n为每包长度中的比特数。
经过上述讨论,常见的三种二进制数字调制,采用不同解调方法其误码率pe与信噪比r的关系如表2-1所示。
表2-1 误码率表

图2-20所示为pe与信噪比r的函数关系,最优信噪比的方式为相干解调下的2PSK,这也是在所有无线调制方法中,抗噪性能最好的调制方式。
通过表2-1中的公式计算可知,当需要保证误码率小于0.1%的二进制数字系统,在最优解调方案下则需要满足:
- 2PSK保证信噪比大于6.8dB(相干解调);
- 2DPSK保证信噪比大于7.3dB(相干解调);
- 2ASK保证信噪比大于12.8dB(相干解调);
- 2FSK保证信噪比大于9.8dB(相干解调)。
2.二进制系统常见调制技术性能对比
1)频带宽度
当码元宽度为Ts时,2ASK系统和2PSK的第一零点带宽为2/Ts,2FSK系统的第一零点带宽为|f1-f2|+2/Ts。因此从频带利用率的角度看,2FSK系统频带利用率不如前两者高。
当码元宽度为Ts时,2ASK系统和2PSK的第一零点带宽为2/Ts,2FSK系统的第一零点带宽为|f1-f2|+2/Ts。因此从频带利用率的角度看,2FSK系统频带利用率不如前两者高。
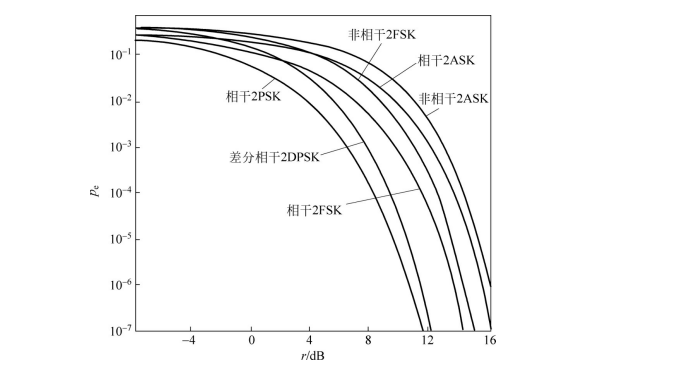
图2-20 误码率pe与信噪比r的函数关系图
2)误码率(高斯白噪声条件下)
相干解调系统抗噪声性能优于非相干解调系统。当r很高时,即r→∞时,每种传输的相干解调与非相干解调趋于同一近似表达式, 说明系统抗噪声性能差异不大。
对于2ASK、2FSK、2PSK系统相干解调时,在相同误码率条件下,在信噪比要求上2PSK比2FSK小3dB,2FSK比2ASK小3dB。
在抗加性高斯白噪声方面,相干2PSK性能最好,2FSK性能次之,2ASK性能最差。2PSK系统抗噪声性能优于2DPSK系统,但它有反向工作现象,故在实际工程中广泛应用2DPSK系统。
3)对信道特性变化的敏感性
在选择数字调制方式时还应考虑它的最佳判决门限对信道特性的变化是否敏感。在2FSK系统中比较两种解调输出的大小来作判决,不需要人为设定门限电平。在2PSK系统中,最佳门限为0,与接收信号的幅度无关,不随信道特性变化而变化,接收机总能保持最佳门限。对于2ASK系统,最佳判决门限与信号及噪声均有关,当信噪比较大时,最佳门限为a/2,它仍与信号幅度有关。因此,信道特性变化时,2ASK方式不容易保证始终工作于最佳判决状态,所以它对信道特性变化比较敏感,性能最差。
4)设备的复杂程度
对于2ASK、2FSK及2PSK三种方式来说,发送端设备复杂程度相差不多,接收端的复杂程度则与所选用的调制和解调方式有关。
相干解调的电路设备要比非相干解调时复杂;而同为非相干解调时,2DPSK的设备最复杂,2FSK次之,2ASK最简单。
5)抗多径
2PSK信号最为敏感,2FSK信号性能较为优越,因此2FSK广泛应用于多径时延较严重的短波信道。