PAPR(Peak-to-Average Power Ratio,峰值平均功率比)是衡量信号峰值功率与平均功率之比的指标。在正交频分复用(OFDM)系统中,由于多个子载波信号的叠加,可能会产生较大的瞬时功率峰值,导致PAPR升高。高PAPR会导致放大器出现非线性失真和频谱扩展,影响信号的传输质量和系统的整体性能。
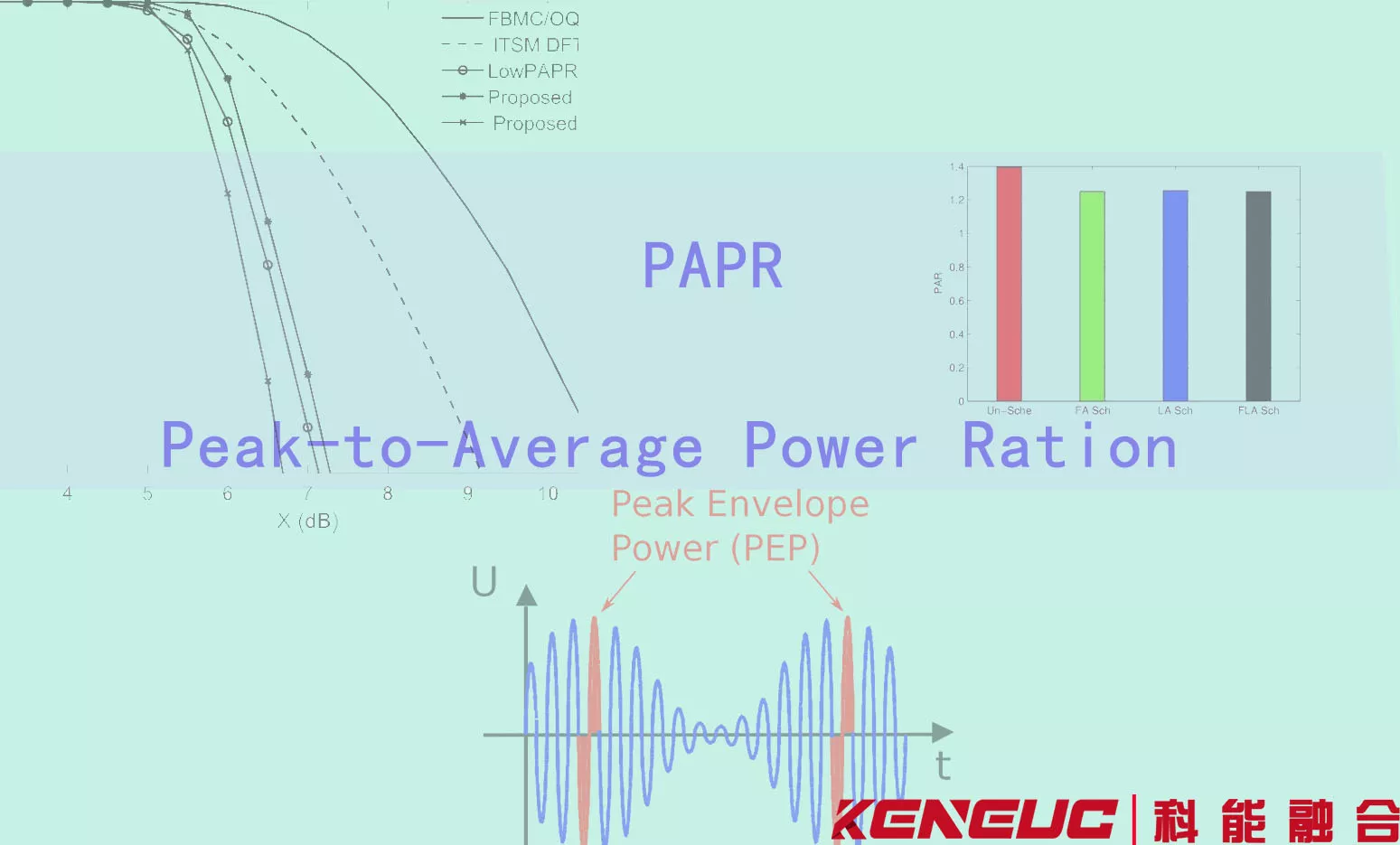
PAPR的高低受多种因素影响,包括子载波的数量、调制方式、信号的相位关系等。当多个子载波相位相同或相近时,叠加信号的瞬时功率峰值会增大,从而导致PAPR升高。此外,功率放大器的动态范围有限,如果PAPR过高,信号容易进入放大器的非线性区域,导致信号失真和频谱扩展。
1. 信号功率特性
平均功率
在探讨信号的功率特性时,平均功率是一个不可或缺的概念。它是衡量信号强度和能量分布的关键指标,尤其在通信系统的设计和分析中发挥着重要作用。
平均功率的计算方法可以根据信号的类型和特点而有所不同。对于周期性离散时间信号x(n),其时域平均功率定义为:
1、Px = (1/N) * Σ[n=0 to N-1] |x(n)|^2
其中,N表示信号的周期长度。这个公式直观地反映了信号在一个完整周期内的平均能量水平。
值得注意的是,平均功率的计算不仅限于时域,还可以通过频域分析来完成。根据Parseval定理,周期信号的时域平均功率等于其频域平均功率:
2、Px = Σ[k=0 to N-1] |ck|^2
这里,ck代表信号的傅里叶级数系数。这种方法为我们提供了一个从频域角度理解信号能量分布的视角。
为了更全面地理解平均功率,让我们通过一个简单的正弦波信号x(n) = cos(2πf0n)为例来进行分析。假设信号周期为N = 1/f0,我们可以计算其时域平均功率:
3、Px = (1/N) * Σ[n=0 to N-1] |cos(2πf0n)|^2
利用三角恒等式cos^2(θ) = (1/2)(1 + cos(2θ)),我们可以推导出:
4、Px = (1/2)
这个结果表明,对于理想的正弦波信号,其平均功率正好等于其峰值功率的一半。这一特性在许多工程应用中具有重要意义,特别是在交流电路分析和功率计算方面。
平均功率不仅是信号分析的基础,还在通信系统设计中扮演着关键角色。例如,在正交频分复用(OFDM)系统中,平均功率的计算对于评估系统性能和优化资源分配至关重要。通过对不同调制方案和编码策略的平均功率进行分析,工程师们可以更好地平衡系统效率和抗干扰能力,从而提升整体通信质量。
此外,平均功率还是计算峰值平均功率比(PAPR)的关键组成部分。PAPR反映了信号瞬时功率与其平均功率之间的比率,是衡量信号动态范围的重要指标。较低的PAPR有利于提高功率放大器的效率,减少信号失真,因此在现代通信系统设计中备受关注。
峰值功率
在探讨信号功率特性时,峰值功率是一个不可忽视的关键概念。它不仅反映了信号的瞬时特性,还在通信系统设计和性能评估中扮演着重要角色。
峰值功率是指信号在某一特定时刻所能达到的最大功率值。对于周期性信号,它通常出现在一个周期内的特定点上。在正弦波信号中,峰值功率恰好等于其平均功率的两倍。这一特性在交流电路分析和功率计算中具有重要意义。
峰值功率的计算公式为:
P_peak = V_peak × I_peak × cos(φ)
其中:
V_peak 代表电压的峰值
I_peak 代表电流的峰值
φ 代表电压和电流之间的相位差
值得注意的是,峰值功率的计算与信号的波形密切相关。对于正弦波,峰值功率等于平均功率的两倍。然而,对于非正弦波,尤其是含有高次谐波的复杂波形,峰值功率与平均功率的比例关系可能会发生变化。这种差异在评估电力系统中的谐波影响时尤为重要。
在实际应用中,峰值功率的测量通常采用专门的仪器设备,如频谱仪或宽带(峰值)功率计。这些设备通过幅度统计功能(APD或CCDF)来测量峰均比,为工程师提供了评估信号动态特性的有力工具。
理解峰值功率对于通信系统设计至关重要。在正交频分复用(OFDM)系统中,高PAPR(峰值平均功率比)可能导致功率放大器工作在非线性区域,引发信号失真和频谱扩展。因此,合理控制峰值功率成为OFDM系统设计的一个关键考量因素。
通过深入理解峰值功率的概念和特性,工程师们可以更好地优化通信系统设计,平衡信号质量和功率效率,从而提升整体系统性能。
2. PAPR与信号功率关系
数学表达
在探讨PAPR与信号功率关系的数学表达时,我们需要深入了解这两个概念的本质及其相互作用。PAPR(峰值平均功率比)是衡量信号功率波动程度的关键指标,而信号功率则反映了信号的能量特征。
PAPR的数学表达式为:
PAPR = E{max(y^2)} / E(y^2)
其中:
y 代表多载波叠加后的信号波形
E 表示期望值运算
max 函数用于确定信号的最大瞬时功率
这个公式清晰地展示了PAPR与信号功率之间的关系。分子部分E{max(y^2)}计算了信号的最大峰值功率,而分母E(y^2)则给出了信号的平均功率。两者之比即为PAPR,反映了信号功率的动态范围。
为进一步量化PAPR与信号功率的关系,我们可以引入累积分布函数(CCDF)的概念。CCDF定义为:
Pr[P > θ] = 1 - F_P(θ)
其中:
P 表示信号的瞬时功率
θ 是给定的阈值
F_P(θ) 是功率的概率密度函数
CCDF曲线提供了信号功率超过特定阈值的概率分布,这在评估系统性能时尤为重要。在实际应用中,我们通常关注0.01%概率下的PAPR值,也称为峰值因子(CF, Crest Factor)。
值得注意的是,PAPR与信号功率的关系还受到多种因素的影响,主要包括:
- 信号调制类型 :不同的调制方案会导致基带信号的峰均比有所不同。例如,QPSK调制通常具有较低的峰均比,而QAM调制则较高。
- 滤波特性 :基带滤波器的特性会影响最终的PAPR值。在WCDMA和TD-SCDMA系统中,即使原本是恒包络的QPSK调制信号,经过根升余弦滤波后也会产生一定的峰均比。
- 载波数量 :对于多载波系统,PAPR与载波数量N之间存在近似对数关系:
PAPR ≈ 10 * log10(N)
这表明随着载波数量的增加,PAPR呈现对数增长趋势。
通过深入理解PAPR与信号功率关系的数学表达,我们可以更好地把握信号功率特性的本质,为后续的系统设计和优化奠定坚实的理论基础。
物理意义
在探讨PAPR与信号功率关系的物理意义时,我们需要深入理解这两个概念如何在通信系统中相互作用。PAPR(峰值平均功率比)作为衡量信号功率波动程度的关键指标,其物理意义体现在多个方面:
1、功率放大器效率 : PAPR的高低直接影响功率放大器的工作状态。较高的PAPR意味着信号的瞬时功率变化较大,可能导致功率放大器工作在非线性区域。这种情况下,放大器的效率会显著降低,因为大部分输入功率无法有效地转换为输出功率。例如,在OFDM系统中,高PAPR可能迫使设计师选择更大功率等级的放大器,以防止饱和,但这又会增加系统成本和能耗。
信号失真 : 当功率放大器工作在非线性区域时,会产生信号失真。这种失真主要表现为两种形式:
- 带内失真 :信号的频谱成分发生畸变,影响信号的质量和可解调性。
- 带外辐射 :信号能量泄漏到相邻频带,造成对其他信道的干扰。
这两种效应都会严重影响通信系统的性能,降低传输速率和可靠性。
2、系统容量和覆盖范围 : PAPR对系统容量和覆盖范围也有间接影响。较高的PAPR要求更大的发射功率预算,以补偿信号传播过程中的衰减。这不仅增加了系统能耗,还可能受到法规限制。同时,高PAPR还会增加接收端的解调难度,尤其是在远距离或弱信号条件下。
3、调制和编码效率 : PAPR还影响调制和编码方案的选择。为了降低PAPR,系统设计者可能需要牺牲一些调制阶数或编码增益,从而影响系统的整体性能。例如,在高阶QAM调制中,虽然可以获得更高的比特率,但同时也伴随着更高的PAPR,这就需要在系统设计中权衡利弊。
通过深入理解PAPR与信号功率关系的物理意义,我们可以更好地把握通信系统设计的关键要素,为优化系统性能和提高能源效率提供理论基础。在实际应用中,工程师们需要综合考虑这些因素,制定合理的系统设计方案,以实现最佳的性能-成本比。
影响因素
在探讨PAPR与信号功率关系的影响因素时,我们需要全面考虑多个方面的相互作用。这些因素共同决定了信号的功率特性,进而影响整个通信系统的性能。以下是影响PAPR与信号功率关系的主要因素:
- 信号类型 :不同类型的信号具有独特的功率分布特性。例如,正弦波信号具有恒定的功率,而脉冲信号则表现出明显的功率波动。这种固有的特性直接影响了PAPR的大小。
- 调制方式 :调制方案的选择对PAPR有着显著影响。
- 滤波特性 :基带滤波器的特性对PAPR有重要影响。即使原本是恒包络的QPSK调制信号,在经过根升余弦滤波后也会产生一定的峰均比。这是因为滤波过程改变了信号的频谱分布,进而影响了功率的瞬时变化。
- 载波数量 :对于多载波系统,如OFDM,载波数量与PAPR之间存在近似对数关系:PAPR ≈ 10 * log10(N);其中N为载波数量。这意味着随着载波数量的增加,PAPR呈现对数增长趋势。
- 星座图映射 :不同的星座图映射方案对PAPR有不同程度的影响。例如,格雷编码可以降低符号间的欧几里得距离,从而在一定程度上改善PAPR特性。
- 交织深度 :交织操作可以在一定程度上平滑信号的功率波动,从而降低PAPR。然而,过深的交织可能会引入额外的延迟,这在实时通信系统中需要权衡。
- 预失真技术 :通过在发射端引入可控的非线性失真,可以抵消功率放大器的非线性效应,从而改善PAPR特性。这种方法虽然有效,但可能会增加系统复杂度。
- 编码冗余 :前向纠错(FEC)编码引入的冗余信息可以在一定程度上降低PAPR,但同时也会降低系统的传输效率。
通过深入理解这些影响因素,我们可以更好地优化通信系统设计,平衡PAPR与信号功率之间的关系,从而提高系统性能和效率。在实际应用中,工程师们需要根据具体场景和需求,权衡各个因素的利弊,以找到最佳的系统配置方案。