自然界中存在着气体、液体或固体,而固体,按其原子排列来说,可以分成品体与非品体两类:按导电能力,则可分成导体、绝缘体和介于二者之间的半导体三种。
通常,把电阻率在10¯6 ~10¯³Ωcm范围内的物质称为导体(如银、铜、铝、铁等金属);电阻率在10Ωcm以上的物质称为绝缘体(如塑料、陶瓷、橡皮、石英玻璃等);电阻率介于导体和绝缘体之间的物质则称为半导体。正是这种半导体,具有重要的特殊的性能,因而才得到广泛的应用。其特性是:
(1)半导体的电阻温度系数一般是负的,它对温度的变化非常敏感,根据这一特性,制作了许多半导体热探测元件。
(2)半导体的导电性能可受极微量杂质的影响而发生十分显著的变化,如纯硅在室温下的电导率为5x10°Ωcm,当掺入硅原子数的百万分之一的杂质时,其纯度虽仍高达99.9999%,但电导率却上升至2Ωcm'.,几乎增加了100万倍!此外,随着所掺入的杂质的种类不同,可以得到相反导电类型的半导体。如在硅中掺入硼,可得到P型半导体;步入锑可得到N型半导体等。
(3)半导体的导电能力及性质会受热、光、电、磁等外界作用的影响而发生非常重要的变化,例如,沉积在绝缘基板上的硫化镉层不受光照时的阻抗可高达几十甚至几百MΩ,但一旦受到光照,电阻就会下降到几十kΩ,甚至更小。
常见的半导体材料有硅、锗、硒等元素半导体,砷化镓(GaAs)、铝砷化镓(GaiAl.As)、锑化钢(InSb),硫化锅(CdS)和硫化铅(PbS)等化合物半导体,还有如氧化亚铜的氧化物半导体,如砷化镓-磷化镓固熔体半导体,以及有机半导体、玻璃半导体、稀土半导体等。利用半导体的特殊性质,可制成光敏器件、热敏器件、场效应器件、体效应器件、霍耳器件、红外接收器件、电荷耦合器件等,以及各种二极管、三极管、集成电路等。
1. 半导体的能带
为了解释固体材料的不同导电特性,人们从电子能级的概念出发引入了能带理论,它是半导体物理的理论基础,应用能带理论可以解释发生在半导体中的各种物理现象和各种半导体器件的工作原理。
1.原子中电子的能级
大家知道,原子是由一个带正电的原子核与一些带负电的电子所组成。这些电子环绕着原子核在各自的轨道上不停地运动着。根据量子论。电子运动有下面三个重要特点。
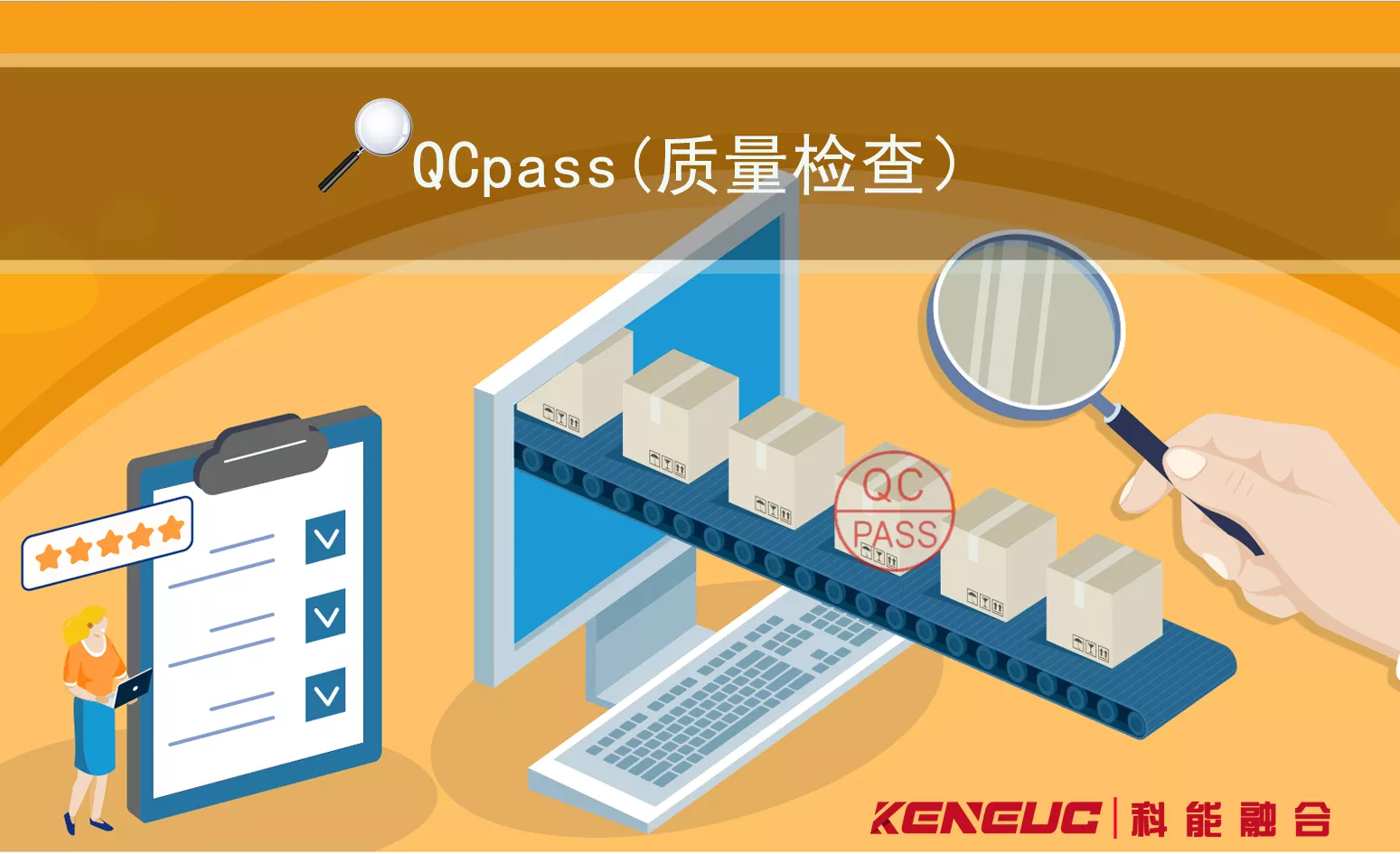
(1)电子绕核运动,具有完全确定的能量,这种稳定的运动状态称为量子态。每一量子态所取的确定能量称为能级。图1-5是硅原子中电子绕核运动的轨道及与其相应的能级示意图。最里层的量子态,电子距原子核最近,受原子核束缚最强。能量最低。越外层的量子态,电子受原子核束缚越弱,能量越高。电子可以吸收能量从低能级跃迁到高能级上去。电子也可在一定条件下放出能量重新落回到低能级上来,但不可能有介于各能级之间的量子态存在。
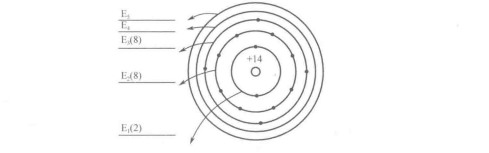
图1-5 硅原子中电子烧核运动轨道及其相应能级示意图
(2)由于微观粒子具有粒子与波动的两重性,因此严格说原子中的电子没有完全确定的轨道,这里的“轨道”所代表的是电子出现概率最大的一部分区域。
(3)在一个原子或原子组成的系统中,不能有两个电子同属于一个量子态,即在每一个能级中,最多只能容纳两个自旋方向相反的电子,这就是泡利不相容原理。此外,电子首先填满最低能级,而后依次向上填,直到所有电子填完为止。


2.晶体中电子的能带
物质是由原子组成的,原子以一定的周期重复排列所构成的物体称为品体。当原子结合成品体时,因为原子之间的距离很近,不同原子之间的电子轨道(量子态)将发生不同程度的重叠。当然,品体中两个相邻原子的最外层电子的轨道重叠最多,这些轨道的重叠,使电子可以从一个原子转移到另一个原子上去。结果,原来隶属于某一原子的电子,不再是此原子私有的了,而是可以在整个晶体中运动,成为整个晶体所共有,这种现象称为电子的共有化。越外层电子的重叠程度越大,且原子核对它的束缚越小,因此,只有最外层电子的共有化特征才是显著的。
晶体中的电子虽然可以从一个原子转移到另一个原子,但它只能在能量相同的量子态之间发生转移,所以,共有化的量子态与原子的能级之间存在着直接的对应关系,因此,N个原子排列起来结合成品体,原来分属于N个单个原子的相同能级必须对应分裂或属于整个品体的N个能量稍有差别的能级。如图1-6所示,这些能级互相靠得很近,分布在一定的能量区域。将这能量区域中密集的能级形象地称为能带,由于能带中能级之间的能量差很小,所以通常可以把能带内的能级看成是连续的。在一般的原子中,内层电子的能级都是被电子填满的,当原子组成晶体后,与这些内层的能级相对应的能带也是被电子所填满的,能量最高的是价电子填满的能带,称为价带。价带以上的能带基本上是空的,其中最低的带称为导带,价带与导带之间的区域则称为禁带。

图1-6 N个原子结合成品体前后的能级状态变化
绝缘体、半导体、导体的能带情况如图1-7所示。一般,绝缘体的禁带比较宽,价带被电子填满,而导带是空的。半导体的能带与绝缘体相似,在理想的绝对零度下,也有被电子填满的价带和全空的导带,但其禁带比较窄,正因为如此,在一定的条件下,价带的电子容易被激发到导带中去,半导体的许多重要特性就是由此引起的,导体的能带情况有两种:一是它的价带没有被电子填满,即最高能量的电子只能填充价带的下半部分,而上半部分空着:二是它的价带与导带相重叠。

图1-7 绝缘体、半导体、导体的能带
值得指出的是,能带图并不实际存在,只是用来说明电子的能量分布情况的。
3.半导体的导电机构
在品体中,根据泡利不相容原理,每个能级上最多能容纳两个电子,因此,要改变品体中电子的运动状态,以便改变电子的运动能量,使它跃迁到新的能级中去,一般需要满足两个条件:一是具有能向电子提供能量的外界作用;二是电子要跃入的那个能级是空的。
由于导带中存在大量的空能级,当有电场作用时,导带电子能够得到能量而跃迁到空的能级中去,即导带电子能够改变运动状态。这也就是说,在电场的作用下,导带电子能够产生定向运动而形成电流,所以导带电子是可以导电的,而填满电子的价带中的电子是不能导电的。如果价带中的一些电子在外界作用下跃迁到导带,那么在价带中就留下了缺乏电子的空位。可以设想,在外加电场作用下,邻近能级的电子可以跃入这些空位,而在这些电子原来的能级上又出现了新的空位。以后,其他电子又可以再跃入这些新的空位,这就好像空位在价带中移动样,只不过其移动方向与电子相反罢了,因此,对于有电子空位的价带,其电子运动状态就不再是不可改变的了。在外加电场的作用下,有些电子在原来热运动上叠加了定向运动,从而形成了电流。
导带和价带电子的导电情况是有区别的,即导带的电子愈多,其导电能力愈强;而价带的电子的空位愈多,即电子愈少,其导电能力也愈强。为了处理方便,我们把价带的电子空位想象为带正电的粒子。显然,它所带的电量与电子相等,符号相反,在电场作用下,它可以自由地在品体中运动,像导带中的电子一样能够起导电作用,这种价带中的电子空位,我们通常称之为空穴。由于电子和空穴都能导电,一般把它们统称为载流子。
(1)本征半导体的能带,完全纯净和结构完整的半导体称为本征半导体,它的能带图如图1-8所示。其中图1-8(a)是假设在绝对零度时,又不受光、电、磁等外界作用的本征半导体能带图。此时,导带没有电子,价带也没有空穴,因此,这时的本征半导体和绝缘体一样,不能导电。但是,由于半导体的禁带宽度E较小,因而在热运动或其他外界因素的作用下,价带的电子可激发跃迁到导带,如图1-8(b)所示,这时,导带有了电子,价带也有了空穴,本征半导体就有能力导电了。电子由价带直接激发跃迁到导带称为本征激发。对于本征半导体来说,其载流子只能依靠本征激发产生,因此,导带的电子和价带的空穴是相等的。这就是本征半导体的导电机构的特性。
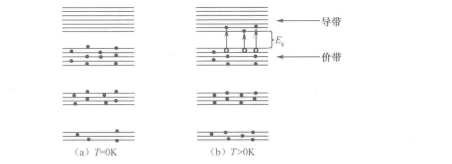
图1-8 本征半导体能带图
(2)杂质半导体的能带,实际上,品体总是含有缺陷和杂质的,而杂质原子上的能级和晶体中其他原子不同,它可以在晶体能级的禁带中,即束缚态的能量一般处于禁带中,如在4价的硅或错品体中,掺入5价原子(如磷、砷、锑等)就可构成N型半导体,5个价电子中有4个价电子与硅原子形成共价键,多余的一个价电子不在价键中,因而容易跃迁到导带成为自由电子,具有这种特点的杂质称为施主杂质,因为它能施予电子,被束缚于施主上的电子的能量状态称为施主能级,如图1-9(a)所示。
如果用具有3个价电子的川族元素(如硼、铝、镓、钢等)的原子取代硅原子组成4个共价键时,尚缺一个电子,即存在一个空的电子能量状态,它能够从晶体的价带接受一个电子,这就等于向价带提供一个空位,这就构成了P型半导体,具有这种特点的杂质称为受主杂质,因为它能接受电子。受主的空能量状态称为受主能级,如图1-9(b)所示。
施主(或受主)能级上的电子(或空穴)跃迁到导带(或价带)中去的过程称为电离,这过程所需的能量就是电离能。图1-9是半导体中杂质能级的示意图。图中E表示导带底,E.表示价带顶。一般,施主能级离导带底较近,即余质的束缚态能级略低于导带底。这样,常温下束缚态中的电子容易激发到导带而使导带中的电子远多于价带中的空穴,一般,受主能级离价带顶较近,即当在半导体中掺入某一杂质而使其束缚态略高于价带顶时,就可在常温下使价带中的电子激发到束缚态,因而使价带中的空穴远多于导带中的电子,由于杂质的电离能比禁带宽度小得多,所以杂质的种类和数量对半导体的导电性能影响很大。
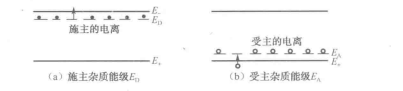
图1-9 半导体的杂质能级
显然,在N型半导体中,一般把电子n称为多数载流子,而空穴p称为少数载流子,即n>pp:而在P型半导体中,则与上相反,多数载流子p>>n(少数载流子)。
2. 热平衡与非平衡载流子及其运动
1.热平衡载流子及费米能级EF
在不变的外界条件下,宏观体系自发地趋向于一种平衡状态,此时表征体系宏观性质的每一参数的数值都不随时间而变化即称为热平衡。这时电子占据某一能量状态E的概率fn(E)也是一定的,这个能量为E的能级被电子所占有的概率fn(E)是根据费米-狄拉克的统计理论得到的,称为费米-狄拉克分布函数,即

式中,k=1.38x102*J/K,为玻耳兹曼常数:T为绝对温度(单位为K);Ef称为费米能级,是热平衡条件下的一个重要参数。当E=Ef时,由式(1-12)得fn(E)=1/22.即在能量等于费米能级的能级上,电子的占据概率为1/2:当E<Ef时,则fn(E)=1/2,即在能量低于EF的能级上,电子的占据概率大于1/2:当E>Ef时,fn(E)<1//2.即在能量高于Ef的能级上,电子的占据概率小于1/2,由此可见,Ef是能级占有与未占有电子的分界线,因而可用来定性描述半导体中载流子的分布。
显然,空穴占据的概率(E)是不被电子占据的概率,即

一般,费米能级在禁带中,E-Ef比KT大得多,对导带能级,室温条件下很容易满足(E-EF)>5kT,因此导带中电子占据的概率为

同理,价带中空穴占据的概率为

从电子的能级密度和统计分布函数,我们可推导出半导体导带的电子浓度n和价带空穴浓度p分别为

式中,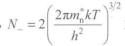 为导带的有效能级密度;
为导带的有效能级密度; 为价带的有效能级密度:mn为自由电子的有效质量:mp为自由空穴的有效质量:h为普朗克常数。
为价带的有效能级密度:mn为自由电子的有效质量:mp为自由空穴的有效质量:h为普朗克常数。
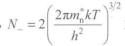 为导带的有效能级密度;
为导带的有效能级密度; 为价带的有效能级密度:mn为自由电子的有效质量:mp为自由空穴的有效质量:h为普朗克常数。
为价带的有效能级密度:mn为自由电子的有效质量:mp为自由空穴的有效质量:h为普朗克常数。
把式(1-16)的n与p相乘。可得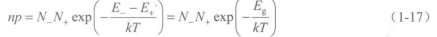
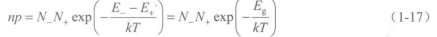
式中,Eg=E--E+为禁带宽度,它是半导体的一个重要参数。
在本征半导体中,电子和空穴浓度相等,即n=p=n,则半导体的本征载流子浓度

由式(1-18)可以看到,在热平衡时,两种载流子浓度的乘积必定等于一个常数,即本征载流子浓度的平方,本征载流子浓度m与温度有关,随着温度升高,m将迅速增大。但只要温度一定,㎡=np也就一定。硅的n1,在300K时为1.5x10¹°c㎡
对于本征半导体,因为,由式(1-16)可解得其费米能级为

通常情况下,N≈N+
这时

由此可知,本征半导体的费米能级E基本上位于禁带的中央,如图1-10(a)所示。
对于杂质半导体,其费米能级E与本征半导体的E在禁带中的位置有所不同,根据统计理论的分析,在极低温度下,N型半导体的费米能级位于施主能级和导带底的正中间,
如图1-10(b)所示;P型半导体的费米能级在受主能级与价带顶的正中间,如图1-10(c)所示。

图1-10 半导体中的费米能级
2. 非平衡载流子及其寿命f
半导体在热平衡状态下,其载流子的浓度有一个恒定的数值。但在外界因素的作用下,例如半导体接受光照,由于光的激发,电子和空穴的产生率大于复合率,这就可能在导带和价带增加载流子(电子和空穴)的数目。这种增加的电子和空穴我们称为非平衡载流子,并用An和辱表示。这样,在导带和价带中电子和空穴的浓度分别为
n=no+△n, p=po+△p (1-21)
式中,no与po分别表示光照前一定温度下热平衡载流子的浓度。
(1) 非平衡载流子的寿命。非平衡载流子△n(或△p)的复合率一般可表示为
复合率=△n/τ(或△p/τ) (1-22)
式中,T为常数,称为非平衡载流子的寿命,T的物理意义有如下三点。
① 寿命T的数值标志着非平衡载流子复合的快慢。这可从式(1-22)可清楚地看到,寿命T越长,复合率越小;寿命,越短,复合率越大。
② T就是当非平衡载流子浓度衰减到原来的i/e所需的时间。在没有外界作用下,非平衡载流子浓度的变化率等于复合率(这里只考虑△n,△p也有同样的形式),即

式中,负号表示复合作用使△n随时间减小。△n是时间t的函数。从式(1-23)容易解得

式中,△n为t=0时非平衡载流子的浓度。当t=τ,其浓度衰减到原来的1/e。

③ t是非平衡载流子的平均存在时间。非平衡载流子是逐步消失的, 为所有非平衡载流子存在时间的总和。而非平衡载流子的总数就是t=0时的数值△n(0)。所以,载流子平均存在的时间为
为所有非平衡载流子存在时间的总和。而非平衡载流子的总数就是t=0时的数值△n(0)。所以,载流子平均存在的时间为

(2) 非平衡载流子的复合。
①自由电子与自由空穴的直接复合,即导带电子直接落在价带空穴的位置上,而与空穴结合失去其自由态的过程。通常,直接复合会辐射出光子来,这种光子的能量等于自由载流子复合时所放出的能量,其数值大致等于晶体禁带宽度。
设n和P分别表示电子和空穴的浓度。每一个电子都有可能和空穴相遇而复合,它们的复合显然和它们的浓度成比例,因此,单位体积内电子、空穴的复合率为
复合率=ynp (1-27)
式中,y称为复合系数或复合概率。在平衡的情况下,复合率等于产生率。则式(1-27)中的n和p即为平衡态载流子no和po.
②通过复合中心的间接复合:由于半导体中晶体结构的不完整性和杂质的存在,在禁带内存在一些深能级,这些能级能俘获自由电子与自由空穴,从而使它们复合,这种深能级称为复合中心。自由载流子通过复合中心复合也往往产生光辐射。
间接复合过程包含两个步骤。
- 电子由导带落入复合中心;
- 电子由复合中心落入价带中的空穴。
从而完成了一对电子-空穴的复合,在每次复合之后,复合中心仍然保持原来的情况,因而它就能不断地起复合中心的作用。
(3)陷阱效应。半导体内的杂质(或缺陷)除了决定材料的导电性质(起施主或受主的作用)和促进非平衡载流子的复合(决定非平衡载流子的寿命)等作用外,还有一种陷阱效应。它和复合中心的作用一样,也是存在着非平衡载流子情况下所发生的一种效应。
施主、受主、复合中心或者其他各种杂质能级,在平衡时都有一定数目的载流子,它们通过载流子的俘获和产生过程保持着平衡。由于某种原因,岀现了非平衡载流子,使这种平衡遭到破坏,这就必然引起杂质能级上的电子数目变化。如果杂质能级上的电子增加,则说明杂质能级有收容电子的作用;如果杂质能级上的电子数减少,则说明杂质能级有收容空穴的作用。杂质能级的这种积累非平衡载流子的作用就叫做陷阱作用。通常,把有显著陷阱效应的杂质能级常简称为陷阱。有显著陷阱效应的典型陷阱有很不相同的电子和空穴的俘获概率:如果某杂质能级俘获电子的概率远大于俘获空穴的概率,则该杂质能级可称为电子的陷阱;反之,可称为空穴的陷阱。
由于陷阱的存在,直接影响着半导体的一些性质。陷阱能俘获电子或空穴而不使它们复合,就增长了载流子的存在时间,这些被陷载流子过一段时间后,在一定条件下,又会重新被激发到导带(或价带),这时才能通过一定的复合机构复合,这样就显著地增长了非平衡到平衡的整个弛豫过程(过渡需要的时间称为弛豫时间)。在陷阱中的载流子被激发成自由载流子后,可能通过复合机构复合,但也可能再次为陷阱所俘获。多次陷落更加延长了弛豫时间。少数载流子陷阱阻碍了少数载流子与多数载流子的复合,因而增加了多数载流子的寿命,从而增加了定态光电导的灵敏度。多数载流子陷阱的存在,减少了多数载流子的数目,当然也就减少了定态光电导的灵敏度。
3. 载流子的运动
半导体中存在能够自由导电的电子和空穴,在外界因素作用下,半导体又会产生非平衡电子和空穴,这些载流子的运动形式有如下两种。
(1)扩散运动。扩散运动是在载流子浓度不均匀的情况下,载流子无规则热运动的自然结果,它不是由电场力的推动而产生的。我们把载流子由热运动造成的从高浓度处向低浓度处的迁移运动称为扩散运动。对于杂质均匀分布的半导体,其平衡载流子的浓度分布也是均匀的。因此,不会有平衡载流子的扩散,这时只考虑非平衡载流子的扩散。当然,对于杂质分布不均匀的半导体,需要同时考虑平衡载流子和非平衡载流子的扩散。
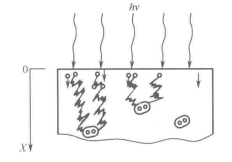
图 均匀半导体中载流子的扩散
现研究一维稳定扩散的情形。例如,光均匀地照射一块均匀的半导体,如图1-11所示。假设光在表面很薄的一层内几乎全部被吸收,而非平衡载流子的产生也局限于这个薄层内。由图可见,在x=0处,因光照而产生的非平衡载流子浓度为明(0)或△"(()),由于在x方向存在浓度梯度,光生载流子将沿x方向扩散,最后在体内复合而消失。只要入射光保持不变,在x=0处Ap(O)与△"(0)也将不变。
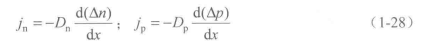
式中,jn和jp分别为电子和空穴的扩散电流密度;Dn和Dp分别为电子和空穴的扩散系数;负号表示扩散流的方向与浓度梯度方向相反。
(2)漂移运动。漂移运动是载流子在电场的加速作用下的一种定向的运动。半导体中晶格原子和杂质离子在晶格点阵位置附近做热运动,而载流子则在晶格间做不规则的热运动,并在运动过程中不断与原子和杂质离子发生碰撞,从而改变其运动速度的大小和方向,这种现象称为散射。当存在外加电场时,使载流子做定向的漂移运动。而由于散射作用,载流子的漂移运动在恒定的电场下具有一个稳定的平均漂移速度。在N型半导体中,漂移所引起的电流密度为
j=nqv (1-29)
式中,j为电流密度;n为载流子密度;q为电子电荷;u为载流子的平均漂移速度。欧姆定律的微分形式为
j=δε (1-30)
式中,δ为电导率;£为电场强度。由此可知,一定的电场强度,就有一定值的电流密度,因而也就有一定值的平均漂移速度,即一定值的£对应于一定值的u。实际上,载流子密度一般不因电场的存在而改变,只有在特殊情况下,当电场强到改变能级或使载流子加速到产生碰撞电离,才会引起载流子密度的变化。因此,电场强度与平均漂移速度关系为
u=μ£ (1-31)
式中,μ称为迁移率,它表示载流子在单位电场下所取得的漂移速度,其单位是cm²/s-V„显然,由上述三个公式可得
δ=nqμ (1-32)
在电场强度£的作用下,载流子所得到的加速度。为
a=q£/m* (1-33)
式中,m*为载流子的有效质量;q为载流子所带的电荷(C)。载流子在漂移运动中,因为散射作用,在每次碰撞之后漂移速度就下降为零。如果两次碰撞之间的平均自由时间为奇tf,则tf以后载流子的平均漂移速度u=atf=tfq£/m*,将式(1-31)代入可得
μ=tfq/m* (1-34)
由此看岀,迁移率与载流子的有效质量与平均自由时间Tf有关,而电子的有效质量刀舌比空穴的有效质量mp小,所以电子的迁移率μn比空穴的迁移率μp大。
(3) 扩散运动和漂移运动同时存在。如扩散运动和漂移运动同时存在,则载流子的扩散系数与迁移率之间有爱因斯坦关系。

尽管爱因斯坦关系是在平衡情况下得到的,但也适用于非平衡的情况。由式(1-35)可以看出,同一种载流子的扩散系数与迁移率之间存在正比例关系,其比例系数与温度有关,它在室温(300K)下为0.026V。因此,很容易从载流子的迁移率来推算扩散系数。
由上述分析还可以知道,在电场作用下,任何载流子(多数载流子与少数载流子)均要做漂移运动。一般情况下,少数载流子远少于多数载流子,因此漂移电流主要是多数载流子的贡献。相反,在扩散情况下,只有光照所产生的少数载流子存在很大的浓度梯度,所以对扩散电流的贡献主要是少数载流子。
3. 半导体对光的吸收
物体受光照射,一部分光被物体反射,一部分光被物体吸收,其余的光透过物体。那些被物体所吸收的光,将改变物体的一些性能。下面分析一下半导体对光的几种吸收。
1. 本征吸收
半导体材料吸收光的原因,在于光与处在各种状态的电子、晶格原子和杂质原子的相互作用。其中最主要的光吸收是由于光子的作用使电子由价带跃迁到导带而引起的,这种吸收就称为本征吸收。电子从半导体价带跃迁到导带是一种本征激发,所以本征光吸收也就是本征激发所对应的光吸收。由于激发,自由电子与空穴的浓度都有了增加。由于价带顶和导带底之间存在有一定的禁带宽度Eg,因此,只有在入射光子的能量大于该材料的禁带宽度时,即hu≥Eg时,才可能发生本征激发。对某一半导体而言,本征吸收存在着一个相应于禁带宽度的长波限Ao,超过这个2o界限,也就是频率更低时,就不能引起本征吸收。λo的表达式为
λo=ch/Eg=1.24/Eg (μm) (1-36)
式中,c为光在真空中的传播速度;h为普朗克常数。
本征吸收是很强的吸收,其吸收系数可达l0'/cm的数量级,因此,实际的光吸收发生在约等于106cm这一薄层内。这说明与光吸收有关的现象,往往会要受到表面状态的影响。
2. 杂质吸收
处于杂质能级中的电子与空穴,也可以引起光的吸收。如图1-12(a)所示,电子吸收光子,会从杂质能级跃迁到导带,而价带中的电子吸收光子会跃入杂质能级,在价带中留下空穴。在这种跃迁过程中,光子能量与本征吸收一样,也存在一个长波限为,即
λo=ch/△Ei=1.24/△Ei(μm) (1-37)
式中,AEi即杂质的电离能。这时,引起杂质吸收的光子的最小能量应等于杂质的电离能,即hv=△EIo.
由于杂质电离能比禁带宽度傀小,所以这种吸收出现在本征吸收限以外的长波区,即在本征吸收限长波侧形成如图1-12(b)所示的吸收带。也就是说,杂质吸收的长波限比本征吸收的长波限长。
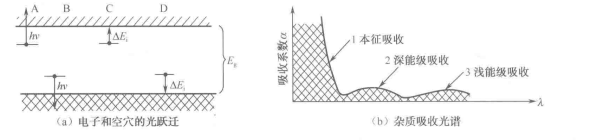
图1-12 杂质吸收
不同的△Ei有不同的长波吸收限λ0,也就是说,只要在半导体中掺以合适的杂质,这种吸收可以在很宽的波段内发生。例如,错掺杂,可以制成截止波长为10〜130μm,范围的快速和高灵敏探测器的材料。
3. 自由载流子吸收
在半导体材料的红外吸收光谱中发现,在本征吸收限长波侧还存在着强度随波长久而增加的吸收。这种吸收是由于自由载流子在同一能带内不同能级之间的跃迁而引起的,因此称为自由载流子吸收。
当半导体处于足够低的温度中时,电子与晶格的联系显得非常微弱,此时吸收的辐射使载流子在带内的能量分布发生显著变化。这种现象虽不引起载流子浓度的变化,但由于电子的迁移率依赖于能量,所以上述过程导致迁移率改变,从而使这种吸收引起电导率的改变。一般吸收系数a与λ的关系(这个关系曲线通常称为物质的吸收光谱)为

按散射理论考虑,n=2,实际n值在1.6〜2.2之间。若杂质含量很大,则n可变到3.5左右。半导体中光子与自由载流子之间发生的动量传递称为光子牵引效应。
4, 激子吸收
在某些情况下,电子在价带中空穴库仑场的束缚下运动,形成可动的电子-空穴对,称为激子。激子的能量小于自由电子的能量,因此能级处在禁带中。激子作为一个整体可以在晶格内自由运动,然而它是电中性的,不能产生电流。
若价带中的电子吸收光子而形成激子时,所吸收光子的波长要比长波限更大些,即在长波限的长波侧形成一些很尖锐的吸收线,每条谱线对应于一定的激发态(〃=1时为基态,&>1时为受激态)。
5. 晶格吸收
在这种吸收过程中,光子直接转变成晶格原子的振动。由于晶体中晶格的振动也是量子化的,即能量的改变量只能取某一些能量值hv的整倍数。
晶格吸收的光谱范围与晶格振动频率在同一数量级,通常波长在10-100μm之间。
4. 半导体的PN结
由上可知,半导体的电学性质在很大的程度上取决于所含杂质的种类和数量。如果把P型、N型、本征(i型)半导体配合起来,结成不均匀的半导体,可制造出各种半导体器件。这里所说的结合,即指一个单晶体内部根据杂质的种类和含量的不同而形成的接触区域,如Pi结、Ni结、PN结等。所谓“结”,严格地说是指其中的过渡区。
1.PN结原理
PN结是将P型杂质和N型杂质分别对半导体掺杂而成的。一般把P型区到N型区之间的过渡区域称为PN结。在PN结的形成过程中,由于空穴浓度在P区比N区高,而电子浓度在N区比P区高。这样,在PN结界面附近就形成了电子和空穴的浓度差,使P区的空穴向N区扩散,N区的电子向P区扩散。这种扩散运动的结果,如图1-13(a)所示,在结与P区界面处出现了电子的积聚,结与N区界面处出现了空穴的积聚。也就是说,在结区中形成了由N区指向P区的内建电场这个电场的出现将产生载流子的漂移运动。
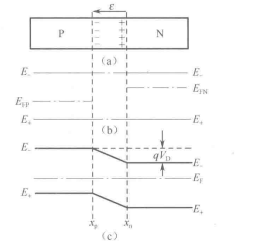
图 热平衡下的PN结
(1)热平衡下的PN结。当PN结处于热平衡时,通过扩散流等于漂移流可以推导出
qVD=Efn-Efp (1-39)
式中,VD通常称为接触电势差或内建电势,它是结区出现的电势差;qVD则称为势垒高度;Efn和Efp再分别表示N型和P型半导体中的费米能级。所以,式(1-39)表示PN结在热平衡下,它们的势垒高度ghj为N型和P型半导体原费米能级之差。由图1-13(c)可以看出,由于热平衡时N型半导体与P型半导体有相同的化学势,因此有统a的费米能级,即平衡过程实际上将两个费米能级拉平了。
(2)非平衡态下的PN结。非平衡态下的PN结的能带如图1-14所示。用n、p表示非平衡状态下的电子和空穴浓度;no与po表示平衡状态下的电子和空穴浓度;△n、△p表示因光照而增加的载流子数。它们之间有如式(1-21)所示的关系。由于电中性的要求,△n=△p在小信号的情况下,△n=△p<<no(或po)。利用式(1-16)和式(1-17)可得

中,qV=Ef--EF+,Ef-和Ef+分别表示在非平衡状态下的电子与空穴的费米能级,称为准费米能级。
由式(1-40)看出,在非平衡状态下,两种载流子浓度的乘积等于平衡态下两种载流子浓度的乘积再乘上一个指数因子 。此因子可以是1,也可以大于或小于1。当f=0时,即平衡态,np=ni²=nopo;当v>0时,即在PN结上加正向电压(或光照),此时np>ni²,说明载流子的浓度增加了,增加的载流子形成结的正向电流;当v<0时,即PN结加反向电压,此时np<ni²,说明载流子比平衡时减少了,减少的载流子将形成结的一部分反向电流。
。此因子可以是1,也可以大于或小于1。当f=0时,即平衡态,np=ni²=nopo;当v>0时,即在PN结上加正向电压(或光照),此时np>ni²,说明载流子的浓度增加了,增加的载流子形成结的正向电流;当v<0时,即PN结加反向电压,此时np<ni²,说明载流子比平衡时减少了,减少的载流子将形成结的一部分反向电流。
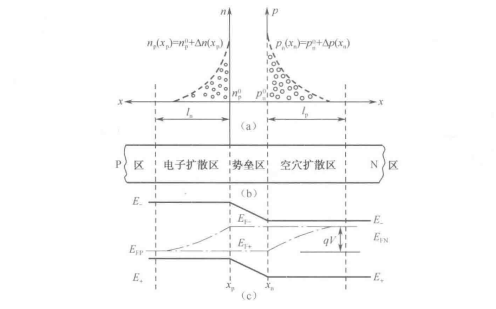
图1-14 非平衡下的PN结能带图
PN结的电流大小可以通过对PN结任一截面的电流来求得,现看通过图1-14中xp处的电流。当施加小于VD的正向电压时,即外加电压抵消一部分VD而使势垒降低,于是就出现了两部分电流:一是从N区向P区注入的电子电流In(Xn):一是由P区向N区注入的空穴电流Ip(Xp),若势垒区中无复合,则In(Xn)=In(Xp)和Ip(Xn)=Ip(Xp)。这样,问题可以简化为纯扩散电流。由此可推证出通过Xp处的电流,即通过PN结的电流。

式中,lo反向饱和电流,是温度的函数。式(1-41)就是PN结的伏-安特性式,是分析所有PN结器件的最基本公式。由于是理想情况下得到的,因此是理想PN结的电流-电压特性。
2.半导体异质结
由两种不同质的半导体材料接触而组成的结,称为半导体异质结。这种结构不仅改变了半导体的禁带宽度,其他如能带结构、载流子有效质量、迁移率等也发生了变化,从而为半导体物理的研究及实际应用开拓了一个新的领域。现在,利用异质结已经制造出许多光电器件,如注入式激光器、发光二极管和太阳能电池等各种类型的光电器件。异质结的构成,不只限于两种不同的半导体材料,对于由金属、绝缘体与半导体构成的结构也可称为异质结,如Ge-GaAs和ZnS-Pt、ZnSeAl-Au、Ge-Si、Gai-xAlxAs-GaAs等。显然,异质结是同质结的引申和发展,而同质结是异质结的特殊情况。
当两种不同的半导体材料构成异质结时,由于它们的晶格常数、电子亲和能与热膨胀系数等各有差异,因此界面处能带的弯曲、界面态密度及势垒宽度等将受到极大的影响。目前,对半导体异质结的研究,着重于它的电流-电压特性及电流的输运机理。在解释异质结性质的模型中,最基本的是由安徒生(Anderson)提出的理想模型。他做了这样两个假设:一是构成异质结的两种材料晶格是完全匹配的,即它们的晶格结构、晶格常数及热膨胀系数相同;二是有不同的禁带宽度£g,介电常数&功函数0及电子亲和能8。
从以上假设可以得到这样的结论:用上述材料构成的异质结,不存在界面态。因此,势垒区的复合可忽略,电流全部是由越过导带或价带的势垒而注入的载流子所引起的扩散流。这样,异质结的讨论,可简化为用类似同质结的理论来进行。
(1)异质结的能带结构。由于构成异质结的两种材料的物理性质有质的区别,这就导致了异质结比同质结有更复杂的能带结构及产生一些同质结所没有的特殊的物理性能。实际上,构成异质结的两种材料的晶格不会是完全匹配的,因此有必要引进一个

式中,ai、a2分别为两种材料的晶格常数。我们将晶格失配小于1%的异质结看做晶格匹配异质结。由P型褚和N型碑化镣组成的异质结的晶格失配小于1%«表1-5是这种异质结的一些主要参数。图1-15就是利用上述参数得到的能带图。其中图1-15(a)是两种材料的独立能带图;图1-15(b)是两种材料组成异质结后,在平衡情况下的能带图。
表1-5N-GaAs-P•Ge异质结材料参数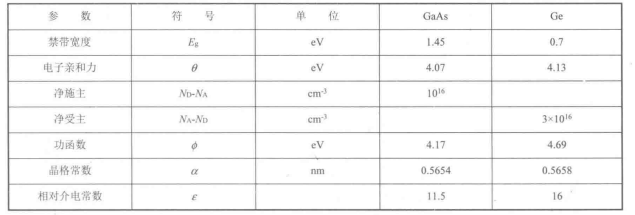

当N-GaAs和P・Ge构成异质结时,它们的能带边缘将是不连续的,如图1-15所示。
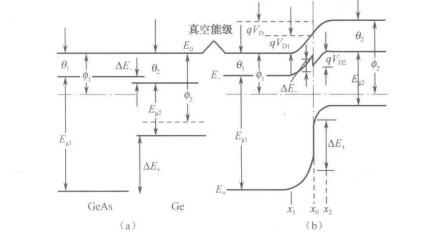
图 1-15 N・GaAs和P・Ge异质结能带图
由于费米能级的差别,必将导致电荷的转移,电子从N型碑化镓移向P型锗,而空穴则由P型锗向N型坤化镓转移,从而在异质结内产生内建电场(电势用4表示)。内建电场阻止电子与空穴的进一步转移,达到平衡态,出现统一的费米能级EF。这样,P・Ge内靠近结区附近形成局部的空穴耗尽区,使能带边向下弯曲。同时,N-GaAs也发生相应的电荷再分布,使能带边向上弯曲。
形成内建电场的电压VD(可理解为PN结中的接触电势,它的值为两种材料费米能级之差)为两个内建电场电压之和,即
VD=VD1+VD2 (1-43)
或
qVD=EF1-EF2 (1-44)
式中,VD1和VD2分别为接触电势VD在材料1、2中的降落。
由于异质结两边的物理参数不同,因此导带底E1、E2和价带顶E+1、E+2的位置不同,而具有差值AE及AE+0。又由于两种材料的掺杂不同,出现了与真空电子自由能级弯曲情况不一致的台阶。即导带和价带岀现不连续性的跃变。其折叠的台阶为:△E=θ1-θ2=△θA;△E+=△Eg~△θ.这就导致导带和价带的势差不同,即电子与空穴的势差不同。实际上,导带底和价带顶的台阶一和△E和△E+与材料的掺杂几乎无关,它反映的只是自由电荷从一种材料脱出进入另一种材料所必须给予的能量。这种能带的不连续性,就是研究半导体异质结能带模型的物理基础。
(2)异质结的电流-电压特性。从安徒生假设出发,由于晶格匹配不存在界面态,因此电流主要是通过结区的扩散流。从图1-15可看岀,阻止空穴从材料2向材料1扩散的势垒高度为q(VD2+VD1)+△E+阻止电子从材料1进入材料2的势垒高度为qVD1,电子的反扩散势垒高度为△E-qVD2。很明显,阻止电子扩散的势垒远比阻止空穴扩散的势垒小。因此,在所讨论的电子与空穴的扩散流中,只须考虑电子的扩散即可。在平衡态下,相反两个方向上的电子扩散流必然相等。由此推证出通过异质结的总电流为

式中,V1=K1U,V2=K2U,分别为外加电压U降落在材料I和2上的数值,而K1与Kz表示U降落在不同材料上的比值,称为分配系数。实际上lo是窄禁带材料中少数载流子的扩散系数及寿命的函数。在一般异质结中,外加电压大部分降落在轻掺杂的宽禁带材料中。因此,V\>V2,式(1-45)括号中的第二项可以略去。这样,在正向偏压下(如光照下)通过结的电流表达式为
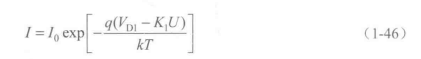
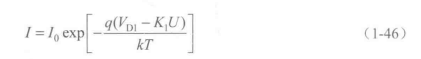
显然,正向电流随外加电压U的变化近似于指数规律。
5. 半导体与金属的接触
半导体与金属的接触,可形成如下的几种情况。
1.肖特基势垒
一般,金属和半导体的逸岀功是不同的,因此它们的犀值不同。当互相接触时,电子就从一个物体流向另一个而使两者都带电,并在界面上形成一个电偶层。金属内含有大量的可移动电子,因此可把偶极层电荷看成表面电荷,但半导体内的载流子数目有限,偶极层电荷必然分布在一个相当深的范围内,即形成一个有一定厚度的空间电荷区。这个区域习惯称为没有自由载 流子的耗尽层。
由于半导体边界上存在空间电荷,因而在能带图中表现为这一层里能带的弯曲。与金属接触并恢复平衡后,金属和半导体这一系统有一个统一的费米能级。在理想情况下,边界面上金属的费米能级与半导体导带底之间的距离不因接触而发生变化,这个距离称为金属-半导体的逸出功ΦBn,此值仅由接触材料的性质决定。此外,离边界相当远处,半导体中的导带与费米能级之间的能量差qVn与接触前的值一样。这些条件决定了金属和半导体接触后会岀现一个高为Vs的势垒。图l-16(a)示出了金属与N型半导体接触前后的能带图。半导体的逸出功θA+qvn小于金属的逸出功Φm,其中θA是半导体表面的电子亲和能。由于这种N型半导体的费米能级高于金属的费米能级,接触后半导体中的电子流向金属,于是在接触面附近的N型半导体中的电子数量减少,形成一耗尽层。这时的垫垒高度为
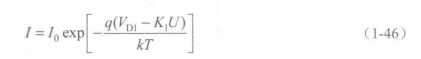
金属-半导体逸出功为
这就是电子由金属进入半导体所遇到的势垒高度。
图1-16(b)所示的是金属与P型半导体接触前后的能带图。这时半导体的逸出功大于金属的逸岀功,即这种P型半导体的费米能级低于金属的费米能级。接触后金属中的电子就要流向半导体与其中的多数载流子空穴中和,造成接触面附近的P型半导体中空穴数量减少,形成一耗尽层,成为空穴势垒。
当加正向偏压VF时,就是使原有势垒降低的偏置,其能带关系如图l-16(c)和图l-16(d)所示。对金属和N型半导体接触而言,就是金属接正极,N型半导体接负极;对金属和P型半导体接触而言,就是金属接负极,P型半导体接正极。当加反向偏压VR时,其偏置的能带图如图1-16(e)和图1-16(f)所示。
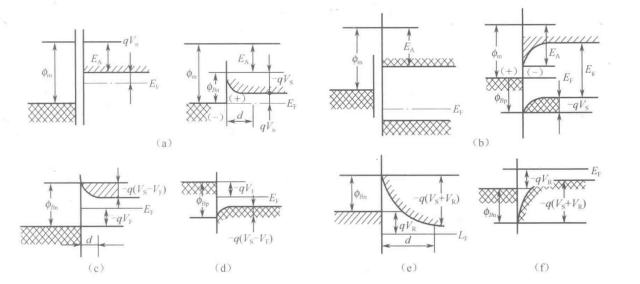
图1-16 金属与半导体的接触及能带图
上面所述的势垒就称为肖特基势垒,能引起肖特基势垒的接触称为阻挡接触。当釆用通常的近似时,可以得到与PN结完全类的电流-电压表达式,即

这里的反向电流/o并非是由载流子的扩散造成的,因为这种结的电流机理是多数载流子越过势垒的热离子发射。
2.注入接触和欧姆接触
图1-17(a)所示的金属与N型半导体的接触与上面讨论的情况相反,这时金属的费米能级高于半导体的费米能级。接触后电子由金属注入半导体中,使半导体边界层内侧的电子浓度大于体内数值,得到一个由电子构成的负空间电荷区。这时,若半导体的长度很短(即一个薄层),由注入引起的负空间电荷区有可能覆盖整个薄层,电流受负空间电荷的强烈影响,使电流-电压曲线呈超线性关系。若半导体的长度较长,则就整体而言仍基本上服从欧姆定律。图1-17(b)所示是金属与P型半导体的接触,由于这里半导体的费米能级高于金属的费米能级,接触后就有电子从半导体流入金属。由平衡条件PN=NI²可知,这将导致空穴密度的增加而形成一正的空间电荷区,因此电流-电压曲线也呈超线性关系。上述这两种接触就称为注入接触。
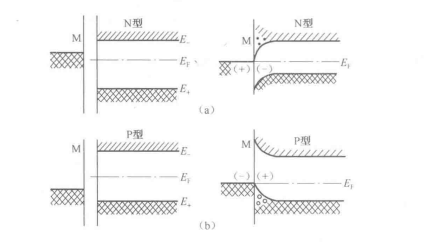
图1-17 金属与半导体的注入接触
若金属与半导体的逸出功相同,接触后没有电荷转移,接触区无电场。加上外电场时,电压-电流(V-I)关系服从欧姆定律,这样的接触称为欧姆接触。在金属与半导体的实际接触中,我们经常要用到欧姆接触,但真正做到欧姆接触较难,因而通常要用注入接触来代替。
声明:优质内容贵在与大家共享,部分文章来源于网络,如有侵权请告知,我们会在第一时间处理。合作交流请加微信