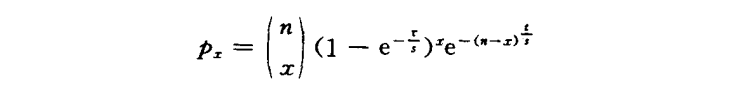决定话务量的另一个重要因素是每次呼叫的占用时长。对电话呼叫的通话时长常采用指数分布,这是符合实际的。
指数分布的分布函数为: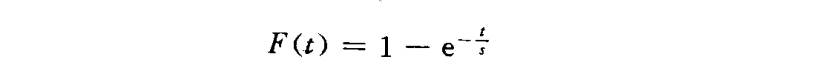
概率密度为: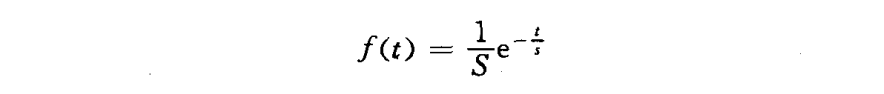
式中S为平均通话时长。
适话时长T为一随机变量,按分布函数的定义,可以得到通话时长7不小于£的概率为:
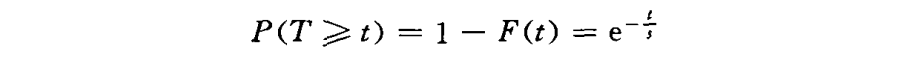
无疑,通话时长T不小于z+r(r为一正数)的概率应为:
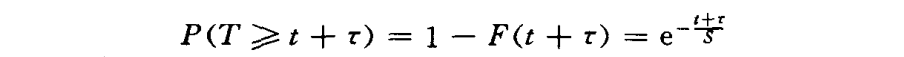
概率P(T^/+r)等于通话时长持续t的概率乘以通话时长持续了Z后,又至少延长r的条件概率P(T^+r/T>t),即:
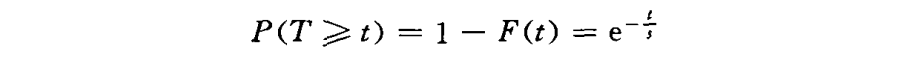
无疑,通话时长T不小于z+r(r为一正数)的概率应为:
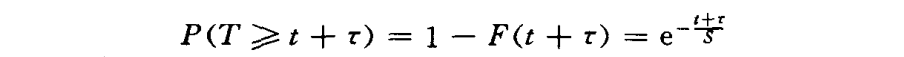
概率P(T^/+r)等于通话时长持续t的概率乘以通话时长持续了Z后,又至少延长r的条件概率P(T^+r/T>t),即:
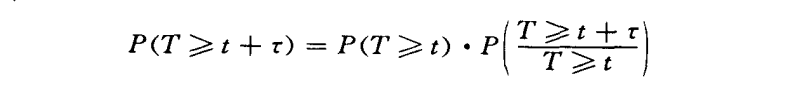
由此可得:
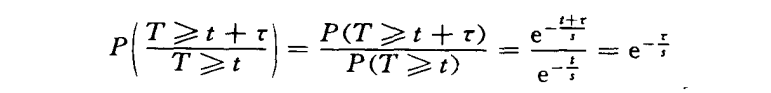
此式说明,一次呼叫的通话时长持续z后又至少延长『的概率仍为指数分布,也就是说,一次呼叫不管通语已进行了多长时间,再延长r时间的概率只决定于r,而与已通话时长无关。一次呼叫的通话时长持续t后又至少延长r的概率eT相当于这次呼叫在r时间内没有释放的概率。如果同时有n个呼叫,则在r时间肉均未释放的概率应为(厂寺)”=£无在t时间内均未释放的概率厂%也就是两个相邻的释放的间隔时间(此间隔时间亦为一随机变量)不小于r的概率,所以相邻释放的间隔时间的分布函数为1-厂号,它的概率密度为ye-7o由此可见,相邻释放的间隔时间亦遵从指数分布,其平均释放间隔为令。正如平均呼叫间隔时间和呼叫强度互为倒数一样,平均释放间隔时间和释放强度也互为倒数,在同时有n个呼叫存在的情况下,释放强度为专。
一次呼叫在r时间内未释放的概率为厂则在r时间内该次呼叫释放的概率应为l-e-7,现在计算在同时有舞个呼叫存在的情况下,在r时间内有工个释放的概率。这个问题可看成是九次贝努里试验,因此所求概率为: