1. 概述
长期以来,人们总是想方设法使信号所占频谱尽量窄,以充分提高频率资源的利用率。 考虑到通信的安全可靠,可采用宽频带信号来传输窄带信息。香农公式是由信息论的奠基人克劳德·香农(Claude Shannon)提出的一种用于计算信道容量的数学公式。该公式可以用来计算在特定信噪比下,信道最大传输速率的理论上限。根据香农公式,信道容量C(以比特每秒为单位)可以通过以下公式计算:C = B * log2(1 + S/N)
其中,B代表信道的带宽(以赫兹为单位),S代表信号的平均功率,N代表信道的平均噪声功率。log2表示以2为底的对数。
克劳德·香农 – 信息论之父

由香农公式可知,在给定信号功率S和白噪声功率”的情况下,只要采用某种编码系 统,就能以任意小的差错概率,以接近于C的传输速率来传送信息。在保持信息传输速率C 不变的条件下,频带B和信噪比是可以互换的。也就是说,如果增加信号频带宽度,就可 以在较低的信噪比的条件下以任意小的差错概率来传输信息。甚至在信号被噪声淹没的情况 下,即S/N< 1或101o& (S/N) <,,只要相应地增加信号带宽,也能进行可靠的通信。
俗话说:“有线的资源是无限的,而无线的资源却是有限的”。无线信道并不是可以任意增加传送信息的速率,它受其固有规律的制约,就像城市道路上的车一样不能想开多快就开多快,还受到道路宽度、其他车辆数量等因素的影响。这个规律就是香农定理(ShannonTheorem)。
2. 1.香农定理意义
香农定理给出了信道信息传送速率的上限和信道信噪比及带宽的关系。香农定理可以解释现代各种无线制式由于带宽不同,所支持的单载波最大吞吐量的不同。
在有随机热噪声的信道上传输数据信号时,信道容量最大值与信道带宽、S/N关系为
式中,C为信道支持的最大速度或者叫信道容量(b/s);B为信道的带宽(Hz);S为平均信号功率(W);N为平均噪声功率(W);S/N为信噪比(dB)。
式(2-19)为香农定理,它给出的是单位时间T=1时的信道容量,当考虑限时T的因素后,香农定理可以变形为
式中,C是信道支持的最大速度或者叫信道容量(b/s);为了区别香农定理,这里用F替代B,同样是信道的带宽(Hz);Ps为信号功率(W);PN为噪声功率(W);S是平均信号功率(W);σ2代表高斯白噪声功率(W)。
图2-35展示了香农定理的物理意义,它给出了决定信道容量C的是三个信号物理参量F、T、 之间的辩证关系。三者的乘积是一个“可塑”性体积(三维),三者间可以互换。
之间的辩证关系。三者的乘积是一个“可塑”性体积(三维),三者间可以互换。
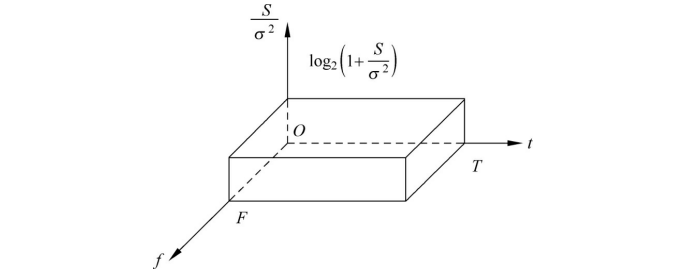
图2-35香农定理的物理意义示意图
3. 2.香农定理用途
根据香农定理,在一个系统内频带、时间、信噪比三者可以互换,可以用公式表示为
式中,F1为系统变化前的频带宽度(Hz);F2为系统变化后的频带宽度(Hz);T1为系统变化前的时间(s);T2为系统变化后的时间(s);γ1为系统变化前的信噪比(dB);γ2为系统变化后的信噪比(dB)。
通过上述公式可以引出如下变化。
1)频带换取信噪比
1)频带换取信噪比
用频带换取信噪比是扩频通信原理中最常用的方法。根据式(2-21):
当,其中称为扩频因子或扩频系数。
频带换取信噪比的应用:
- LoRa技术就是使用频带换取信噪比的方式实现高灵敏度的。
- 雷达信号设计中的线性调频脉冲,模拟通信中的调频优于调幅,且频带越宽,抗干扰性就越强。
- 数字通信中,伪码(PN)直扩与时频编码等,带宽越宽,扩频增益越大,抗干扰性就越强。这在ZigBee技术物理层是采用伪码(PN)直接扩频实现的。
- 深空通信中(功率受能源限制,频谱资源相对丰富),采用两电平数字通信方式有效利用信道容量。
2)信噪比换取频带
用信噪比换取频带为多进制、多电平、多维星座调制方式的基本原理。它利用高质量信道中富裕的信噪比换取频带,以提高传输有效性。
在生活中经常遇到如QAM、MASK、MPSK等都是采用信噪比换频带的方式实现的。人们熟悉的Wi-Fi技术就是采用QPSK、16QAM、64QAM,现在的Wi-Fi6已经采用1024QAM将信噪比换带宽用到了极致。人们熟悉的蓝牙4、蓝牙5、ZigBee等都是用了该策略提升带宽和速率。
图2-36中有4种MQAM方式,包括4QAM、16QAM、64QAM和256QAM,原来1b的能量分别分配到2b、4b、6b、8b中,其传输速率大幅增加。
许多人在想,既然可以实现1024QAM,那么是否可以实现更高的信道容量呢?事实上在信噪比一定的情况下,其信道容量是有限度的。根据式(2-21),在增加信道通带的宽度而不改变信号的平均功率的情况下其增大信道容量的极限为
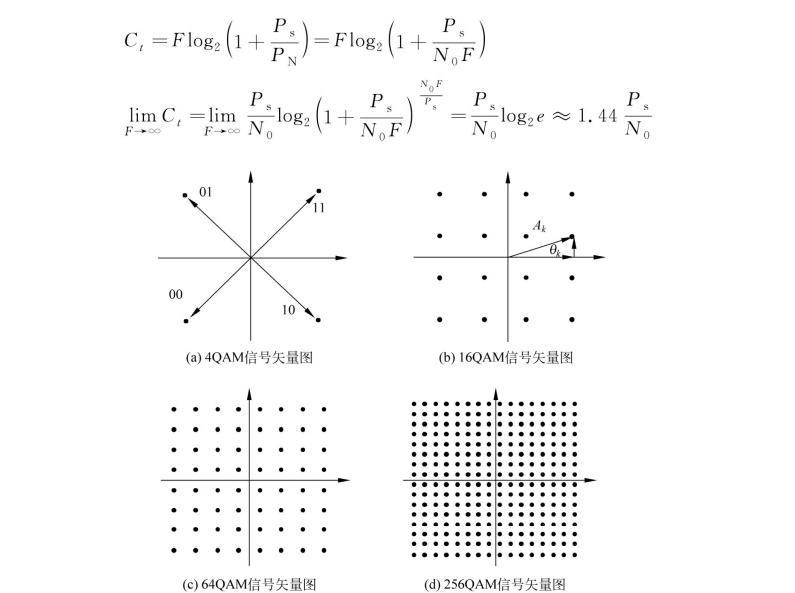
图2-36MQAM星座图
如图2-37所示,不改变信号平均功率的情况下,香农定理的信道极限为1.44Ps/N0,无论F如何增大,信道容量Ct不变。
3)用时间换取信噪比
用时间换取信噪比:带宽固定则有F1=F2,根据式(2-21)可得:
T1log2(1+γ1)=T2log2(1+γ2)
若T2>T1,则γ1>γ2。
重传、弱信号累积接收基于这一原理。如图2-38所示,t=T0为分界线,信号功率S有规律随时间线性增长,噪声功率σ2无规律,随时间呈均方根增长。NB-IoT技术就是利用此方法多次重传用时间换取信噪比。
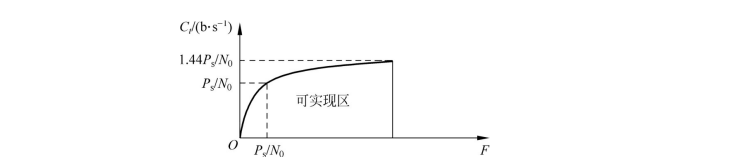
图2-37香农定理信道容量极限
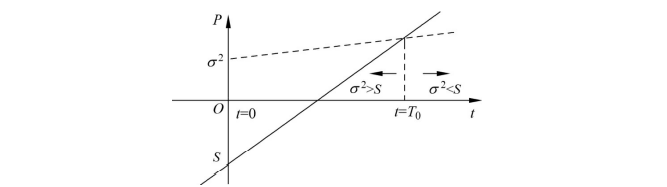
图2-38用时间换信噪比示意图
4)时间换频带、频带换时间
用时间换取频带或用频带换取时间:信噪比相同γ1=γ2,根据式(2-21)可得:
时间换频带、频带换时间可以分别实现如下两种应用:
- 扩频:缩短时间,应用于通信电子对抗、潜艇通信。
- 窄带:增加时间,应用于电话线路传图像。
4. 总结
香农公式的核心思想是利用信号与噪声之比来确定信道的容量。当信噪比较高时,可以传输更多的信息,因此信道容量也会更大。而当信噪比较低时,信道的容量将受到限制。
香农公式在通信系统设计和优化中具有重要作用。它可以提供一个理论上的参考,帮助工程师评估特定信道条件下的最大传输速率,从而指导系统参数的选择和性能的改进。
需要注意的是,香农公式只给出了信道的理论上限容量,实际应用中还需要考虑其他因素,比如编码、调制方式、信号失真等,以及具体的实际场景和应用需求。





