光是电磁波它具有电磁波的通性。因此,光波在光纤中传输的一些基本性质都可以从电磁场的基本方程一麦克斯韦方程组推导出来。一般的求解方法是由麦克斯韦方程组推导出光在均匀介质中的波动方程,经过简化后的波动方程为
式(9-11)、式(9-12)中。μ0为光波导介质(或真空)的导磁率;ε为光波导介质的介电系数。如果电磁场作简谐振荡,由波动方程可以推出均匀介质中的矢量亥姆霍兹方程
式(9-13)、式(9-14)中以。k0=2π/λ是真空中的波数;λ是真空中的光波波长;n为介质的折射率。
在直角坐标系中,E、H的x、y、z分量均满足标量的亥姆霍兹方程
式(9-15)中ψ代表E或H的各个分量。
在光纤的分析中,求上述亥姆霍兹方程满足边界条件的解,即可得到光纤中的场的解答。求解的方法主要有两种:标量近似解和矢量解。


(1)标量近似解
在分析阶跃光纤和渐变光纤时,近似方法之一为标量近似解。这种方法可使分析大为简化.其结果也比较简单,便于应用。
分析阶跃光纤时,假设光纤里的横向(非光传输的方向)电磁场的幅度满足标量亥姆霍兹方程,求出近似解。这是一种近似,其前提是光纤的相对折射率差△很小。△很小的光纤称作弱导波光纤,一般阶跃光纤可以满足这一条件。
分析渐变光纤时,假设纤芯的尺寸无穷,边界不起作用,然后假设横向(非光传输的方向)电磁场的幅度满足标量亥姆霍兹方程,求出近似解。
釆用这一解法可以得到光纤中各个模式的传输系数、模式的截止条件、单模传输条件、多模传输时的模式数量、模式功率分布等的简便计算公式。还可以利用这一方法来分析光纤的色散特性。
采用标量近似解得到的光纤中的模式为标量模。
(2)矢量解
矢量解是求满足边界条件的矢量亥姆霍兹方程的解答。矢量解中各个分量在直角坐标系中都满足标量的亥姆霍兹方程。
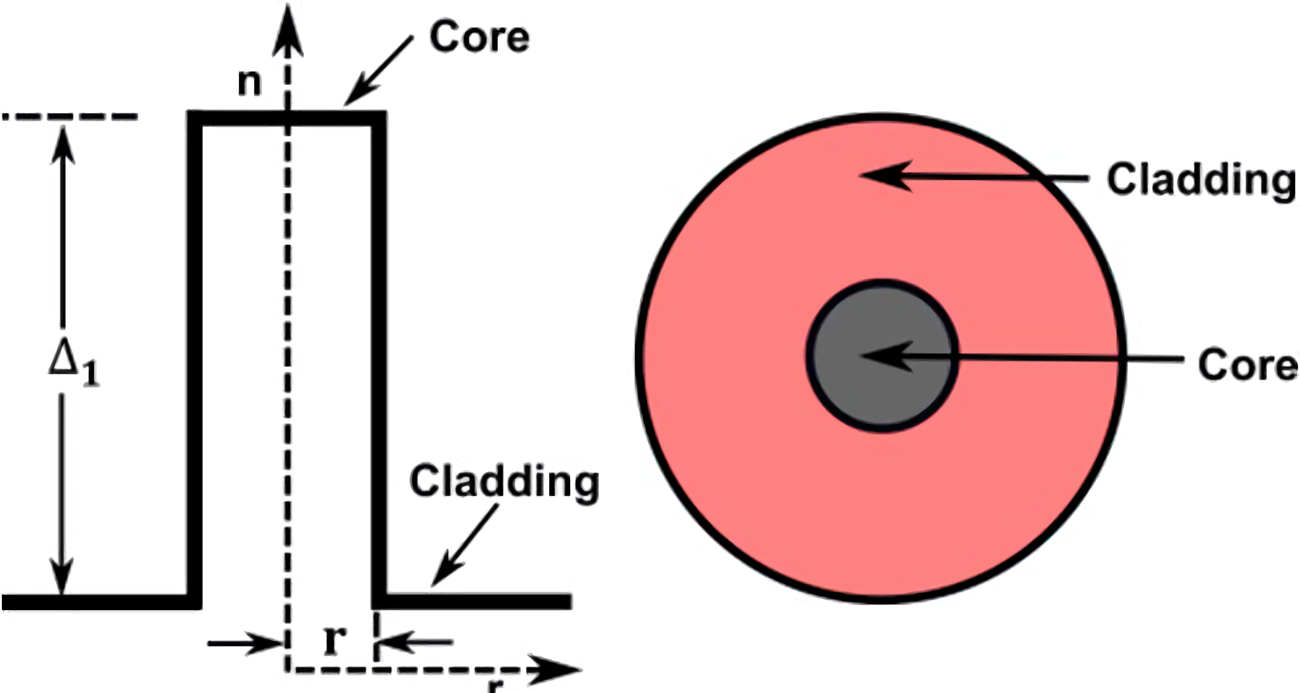

在分析阶跃光纤时,纤芯和包层的折射率都是均匀的,所以矢量解是严格的分析方法,它可以得到精确的模式及场分布,但是比较复杂。对于渐变光纤,需要作一些近似假设,分析仍然十分复杂,需进行数值计算。
采用矢量解得到的光纤中的模式为矢量模式。





